0   引言

超高速飞行器周围形成的激波对气流具有强烈的压缩加热作用，激波层内高温气体发生内能级激发、离解、电离和复合等复杂的物理化学过程，在更高速条件下还会伴随转动能级跃迁、振动能级跃迁、电子能级跃迁等不同的辐射跃迁过程，激波层成为对飞行器加热的强辐射体^[1]。如Apollo再入，辐射加热达到总加热的30%左右。在这种超高速条件下，气体辐射在热防护设计中变得非常重要。

气体辐射加热一直是深空探测领域的重要研究课题。自20世纪50年代末开始，从探月返回条件下的地球再入，到火星返回条件下的地球再入，以及其他行星进入，如金星和火星，辐射加热的实验技术和计算模型^[2]得到持续发展。从最初求解近似无粘流场和透明或灰体气体辐射，发展到耦合化学平衡的粘性流场和半精细非灰光谱模型，随后热力学和化学非平衡流场求解技术的发展和应用^[3-5]促成了非平衡辐射模型的建立^[6-7]。气体辐射测试技术的发展为流场和辐射计算模型的验证、改进和新模型的提出创造了可能性。

气体辐射定量化测试难度非常大，受到实验设备、光学成像系统等各方面的限制。NASA Ames研究中心的EAST(Electric Arc Shock Tube，电弧激波管)开展了大量空间和光谱高分辨的辐射测量实验^[8]，促成了一系列非平衡模型和反应速率的修正与改进。CUBRC(Calspan-University at Buffalo Research Center)的LENS激波/膨胀风洞^[9]、昆士兰大学的X2膨胀管^[10]和JAXA的HVST(High Velocity Shock Tube)激波管^[11]，均开展了气体辐射测量实验。

近年来的辐射实验研究表明，目前的流动和辐射计算模型不确定性仍较大，并且部分实验数据也存在不准确的问题。Brandis等^[12]于2016年在模拟地球大气环境中对激波速度8.0~11.5km/s的真空紫外至近红外的空间、光谱分辨的辐射强度进行测量，与数值结果对比发现，在不同的激波速度下，LAURA/HARA辐射热流计算结果最大高估40%、低估12%，DPLR/NEQAIR最大高估50%、低估20%。数值模拟与实验数据偏差较大，均超过实验标准差31%，表明计算模型仍需完善。2017年，Cruden等^[13]对激波速度7~9km/s、光谱范围190~1450nm的空气非平衡辐射进行了测量。发现考虑不同反应速率的DPLR/NEQAIR对实验数据的复现结果较差，通过分析差异来源对NEQAIR的非玻耳兹曼模型和反应模型进行了改进，提高了数值模拟和实验的符合度。Brandis等^[14]对激波速度4.7~8.0km/s的CH₄/N₂混合气体及纯N₂进行了辐射强度测量，发现新的实验数据量值均高于以往的实验数据，有些甚至高出1个量级，表明目前的气体辐射定量测试还存在不确定性，以此为基础进行的数值模型改进可能也不够准确。作者最后给出了以往实验中可能导致数据误差的原因，并发布了新的数据库用以和数值模型对比。Brandis和Cruden^[15]在2018年发表的文章中给出了纯净N₂在激波速度6~11km/s的辐射强度测量结果，包括平衡光谱辐射强度、给定波长范围的辐射强度空间变化和平均非平衡光谱辐射强度，以及来流参数、激波运动函数等信息，希望引导基于这些结果的代码比较。

综上，气体辐射强度的定量测试和数值计算均未完善，实验结果可能存在误差，计算模型需要改进，迫切需要更为准确和精细的实验数据支撑。因此，针对气体辐射在富氮气环境的地球再入和泰坦进入等热防护设计中引起的不确定性，开展氮气气体辐射实验研究，发展气体光谱辐射强度定量化测试手段，和不同机构及设备的实验结果共同为数值模型提供基础数据，验证与改进计算模型和方法，构建更为完善的气体辐射评估体系，提高对气动物理复杂效应机理的认知，支撑深空探测工程研究。

1   研究方法

1.1   实验设备与方案

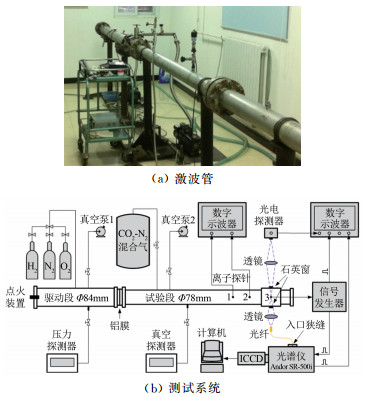
气体辐射强度测量实验在中国科学院高温气体动力学国家重点实验室(LHD)的氢氧燃烧驱动型激波管上开展，实验设备见图 1(a)。激波管运行时产生的高速激波能够模拟飞行器头部脱体激波及波后流场，从而获取波后高时间、空间分辨率的分子、原子谱线特征及其量化数据。

图  1  激波管设备和测试系统示意

Fig.  1  Demonstration of the shock tube and experimental setup

下载: 全尺寸图片 幻灯片

图 1(b)为测试系统示意图。激波管的驱动段与测试段由膜片分隔。试验段内径78mm，可充入空气、氮气、二氧化碳或其他混合气体，以模拟飞行环境介质。试验段尾部设有多对光学窗口，可进行辐射测量、发射光谱诊断和非平衡温度测量。通过调节试段或驱动段压力可获取不同的激波速度，实验中以一组间距1.2m的离子探针进行激波速度的测量，激波速度测量值与理论值的最大误差不超过±2%。

1.2   定量化辐射测试技术

高温气体波长分辨的发射光谱使用光谱仪进行采集，通过对光强响应进行绝对辐射强度标定完成定量化测试。绝对辐射强度标定的理论较为明确，但在具体实现中存在困难^[8]，主要表现在具体的实验设备(包括直径、窗口尺寸和透过率)、采集光路(包括透镜、光阑、狭缝、光纤)等对标定的影响。离线标定往往会带来很大误差，因此激波管实验中的辐射强度标定必须使用原位标定方法。

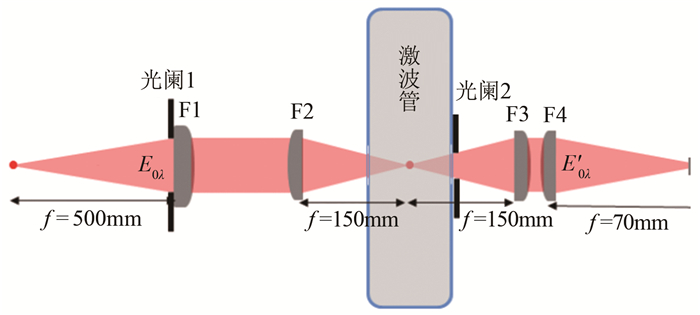
图 2是原位标定系统光学示意图。原位标定系统包括已知辐射照度的标准钨灯光源、光阑、透镜组、光谱仪等。透镜F1、F2、F3和F4的焦距分别为500、150、150和70mm。透镜F1和F2组成的光路系统将标准钨灯光源成像于激波管中心，透镜F3和F4组成的光路将成像汇聚于狭缝处，由光谱仪采集并输出为不同波长的响应。原位标定的主要技术难点在于所有光学部件均需精确设计，以同时保证：(1)透镜F1和光阑1满足标准光源的立体角限制；(2)透镜F2满足激波管窗口尺寸和聚焦点位置限制；(3)光阑2和透镜F3满足光谱仪采集立体角限制；(4)透镜F4和光谱仪狭缝满足光谱仪内部立体角限制。只有精确设定各光学部件的参数才能保证原位标定获得的响应系数是精确的。

图  2  激波管辐射定量测试实验的原位标定系统和仪器示意图

Fig.  2  Schematic diagram of in-situ calibration system for absolute radiation measurement in shock tube

下载: 全尺寸图片 幻灯片

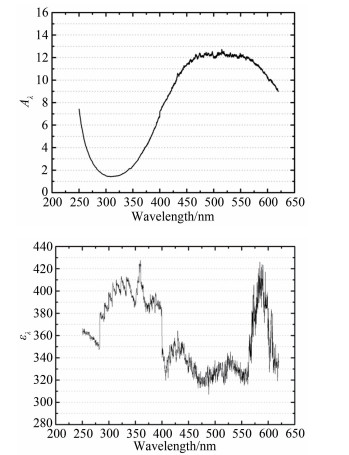
光谱仪的绝对辐射标定可用式(1)描述，其中DN_λ为波长λ处的输出信号(相对值)，A_λ为波长λ的响应系数，R_λ为波长λ的入射照度(绝对值)，ε_λ为系统偏置，Δt为积分时间。根据已知的钨灯辐照度可获得R_λ，通过改变不同的积分时间和狭缝大小，即可标定光谱响应系数A_λ和系统偏置ε_λ。实际测量中，认为Δt=0 (实验中设为100ps)时采集到的信号为背景偏置噪声。图 3为标定后获得的A_λ和ε_λ在200~600nm范围内的变化曲线，激波管实验运行前后进行了多次标定，结果表明标定系数具有良好的重复性。

图  3  响应系数和系统偏置的标定结果

Fig.  3  Calibration results of response coefficient and system bias

下载: 全尺寸图片 幻灯片

1.3   数值模型与方法

激波管氮气辐射强度的数值模拟包括流场、电子态布居和光谱计算^[16]。流场计算得到激波层内每个空间点处的组分数密度和温度，在此基础上进行电子态能级分布计算，最后依据不同的辐射机制得到与频率相关的发射和吸收系数。

1.3.1   流场计算

流体力学求解三维化学反应Navier-Stokes方程，连续性方程为各组元连续性方程，同时包含化学反应源项：

其中，ρ_i为各组分密度，i=1, …, ns。ns为气体组分个数，ρ为总密度，u, v, w分别为x, y, z方向速度，p为压力，E为单位质量总能量。

热力学参数C_p、e、h和输运系数μ、k、D通过拟合温度多项式得到，混合气体参数由Wilke公式计算得到。化学反应源项采用有限速率化学反应模型。气体辐射发生在高温激波层，流场伴随剧烈的离子化反应，辐射也与气体组分紧密相关，因此化学非平衡过程必须使用更复杂的反应模型。本文采用Gupta的11组分(O₂，N₂，O，N，NO，NO⁺，O₂⁺，N₂⁺，O⁺，N⁺，e^-)、19反应模型^[5]。对于氮气介质，该反应系统简化为5组分(N₂，N，N₂⁺，N⁺，e^-)、4反应。

算法方面，对流项采用Van-Leer格式，其中半点值通过使用Van-Albada限制器的MUSCL方法得到；粘性项采用二阶中心格式；时间推进采用LU-SGS和Runge-Kutta方法。

1.3.2   辐射特性计算

在流场求解的基础上进行电子态布居计算，根据原子束缚-束缚跃迁(原子线谱)、原子束缚-自由跃迁(光致电离)、原子自由-自由跃迁(韧致辐射)和分子束缚-束缚跃迁(分子带谱)等机制，计算与频率相关的发射和吸收系数。氮气及其反应产物主要的辐射机制为电子跃迁谱带系，主要包括：N₂第一正系(B³Π_g→A³Σ_u⁺)、第二正系(C³Π_u→B³Π_g)，N₂⁺第一负系(B²Σ_u⁺→X²Σ_g⁺)，N原子的谱线辐射及连续辐射。电子跃迁谱线吸收系数的计算公式为：

式中|R_e(r _{υ′, υ ″}) |²为电子跃迁矩阵元；q(υ′, υ″)是Franck-Condon因子；S_J″Λ″^J′Λ′是线性强度因子；N′ _{e, υ, J}是分子在低能态的数密度；η₀为中心频率的波数；F(η)是谱线线型函数。

2   实验结果与验证

对激波波后N₂气体辐射强度绝对值进行波长分辨的测量。每次实验前进行响应系数的标定，激波管运行时使用光谱仪在同样的实验光路和参数(包括曝光时间、狭缝、增益)条件下记录波后气体辐射量，利用实验前标定的响应系数获得气体随波长变化的绝对辐射强度曲线。

2.1   平衡光谱辐射强度测量与计算

激波管被驱段充入压力800Pa的纯N₂。实验中通过离子探针测得的激波速度范围为5.49~5.70km/s。光谱仪采集区间为290~340nm波段，狭缝0.4mm，1200刻线，积分时间500ns，相应的光谱分辨率为0.25nm。由于单个车次中仅能进行一次数据采集，故实验中对同一状态进行多次重复性实验，每次以不同的触发延迟时间来获取波后不同位置的辐射强度。

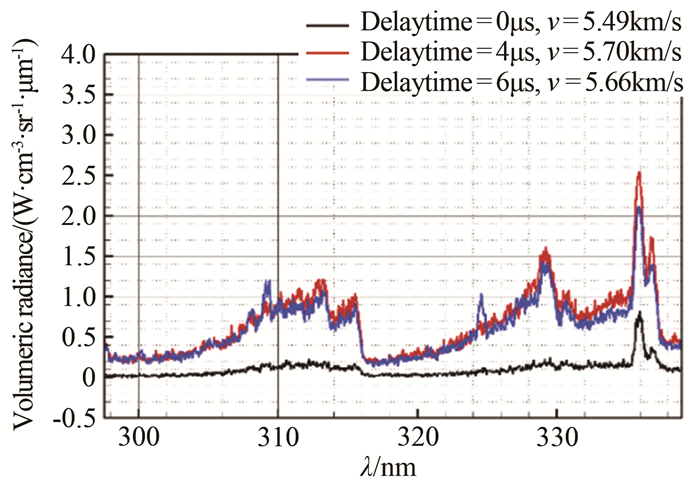
图 4为不同延迟时间得到的体积光谱辐射强度随波长的变化。0μs为激波达到观测位置的时刻，辐射强度近似为0。延迟时间4和6μs测得的波后气体辐射能量密度沿波长的变化基本相同。

图  4  800Pa、5.70km/s状态的N₂辐射强度定量试验结果

Fig.  4  Quantized radiance measurement of N₂ at 800Pa, 5.70km/s

下载: 全尺寸图片 幻灯片

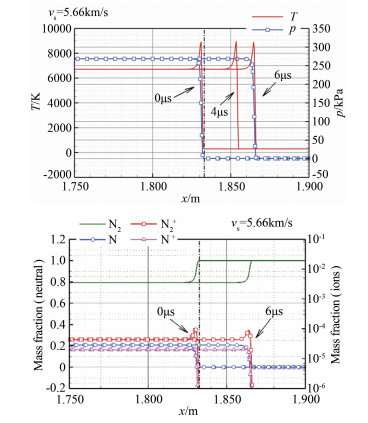
图 5是激波运动速度为5.66km/s的流场计算结果，波速与实验测量结果接近。设定x=1.833m为测点，激波运动至该位置为起始时刻0μs，图中以点划线表示。通过非定常计算推进时间4和6μs，提取x=1.833m位置处的气体状态参数，并进行辐射特性计算。该位置已处于激波后平衡区域，4和6μs延迟对应的波后位置处的压力和温度均相同。组分质量分数曲线中为显示清晰，省略了4μs延迟结果。从6μs曲线观察，波后N₂约有20%分解，主要生成N，也有微量的离子N₂⁺和N⁺生成。

图  5  激波速度5.66km/s的流场参数计算结果

Fig.  5  Computational results of flow parameter at shock velocity 5.66km/s

下载: 全尺寸图片 幻灯片

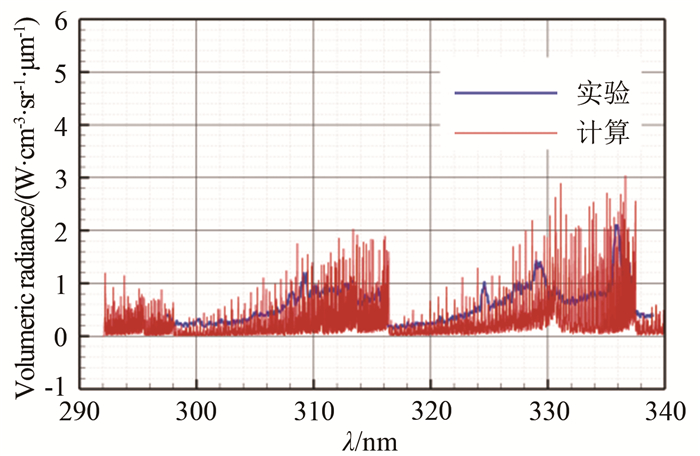
辐射特性计算得到290~340nm范围内的体积辐射强度随波长的变化，和实验结果的对比见图 6。计算结果和实验数据吻合很好，验证了数值计算模型和方法。值得注意的是，在320~330nm附近计算的辐射强度略低于实验值，此波长范围是N₂⁺辐射的主要发射范围，故进行不同组分辐射发射强度的比较。

图  6  6μs延迟的辐射强度计算结果和对比

Fig.  6  Comparison of radiance between computation and experiment at 6μs time delay

下载: 全尺寸图片 幻灯片

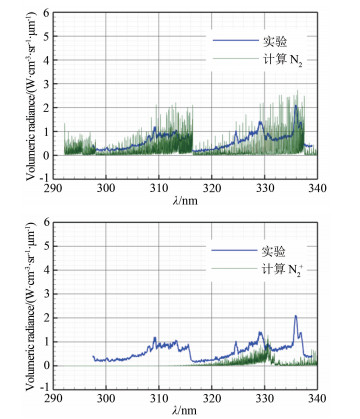
图 7分别是N₂和N₂⁺的光谱辐射强度分布与实验的对比，其余组分在此光谱范围内无辐射。虽然N₂⁺的质量分数比N₂小若干数量级，但其辐射能力较强，在320~330nm波长范围内产生了与N₂在其他波长量值相当的辐射，可见对N₂⁺微量离子质量分数的精确预测对辐射计算结果影响巨大，在320~330nm范围内需进一步研究以确定实验与计算的误差来自于实验测量的准确性，还是计算模型的精度。

图  7  6μs延迟不同组分的辐射强度计算结果和对比

Fig.  7  Comparison of radiance between computation emitted from different species and experiment

下载: 全尺寸图片 幻灯片

2.2   非平衡光谱辐射强度测量与计算

第二组激波管被驱段充入500Pa压力的N₂，适当调整驱动压力，从而达到更高的激波速度。实验中测得激波速度范围为5.75~6.25km/s，高于前述实验状态。光谱仪参数不变，波段290~340nm，光谱分辨率0.25nm。

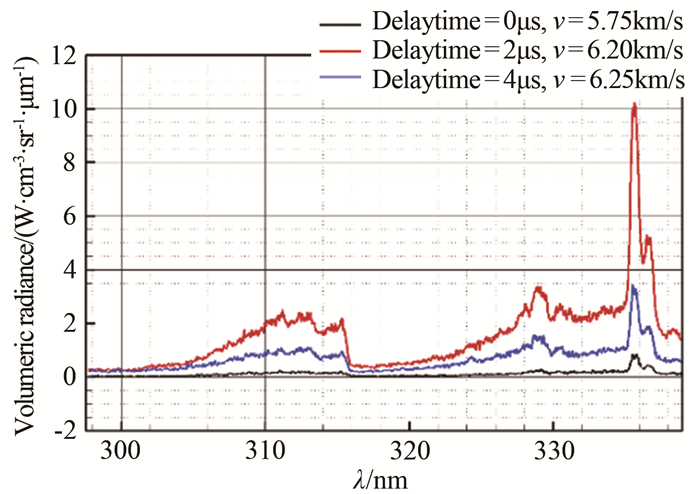
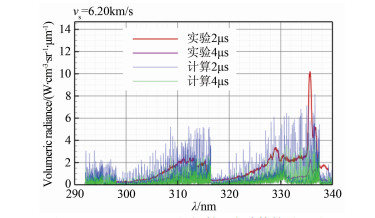
图 8是波后不同位置处的辐射强度测量值沿波长的分布。0μs是激波抵达观测位置的时刻，对更贴近激波位置的2和4μs延迟时间的辐射强度进行测量，结果表明，更高的激波速度条件下，辐射强度比图 4所示更大。同时，2μs延迟的辐射量明显大于4μs延迟的结果。

图  8  500Pa、6.20km/s状态的N₂辐射强度定量试验结果

Fig.  8  Quantized radiance measurement of N₂ at 500Pa, 6.20km/s

下载: 全尺寸图片 幻灯片

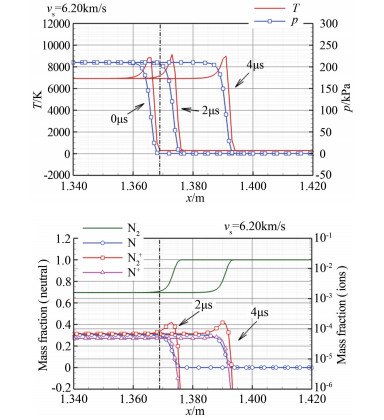
图 9是激波速度6.20km/s的流场参数计算结果。该状态下波后温度比第一组实验略高，压力略低，N₂约有30%分解，高于第一组实验的20%。波后同样主要生成N，离子产物较少，但N₂⁺的质量分数比第一组实验高约1倍。计算中设定x=1.369m为测点，激波到达该位置为起始时刻0μs。时间推进2μs的结果显示该位置仍处在波后非平衡区，温度和组分质量分数皆不同于4μs延迟的平衡区，非平衡区内气体温度略高、离子数密度略大。

图  9  激波速度6.20km/s的流场参数计算结果

Fig.  9  Computational results of flow parameter at shock velocity 6.20km/s

下载: 全尺寸图片 幻灯片

提取不同延迟时间在测点x=1.369m的流动参数进行气体辐射计算，得到如图 10所示的光谱辐射强度随波长的变化曲线，以及和实验值的对比。计算和实验结果符合较好。不同延迟时间的计算结果同样显示出辐射强度的明显差别，这是非平衡区与平衡区的温度和组分浓度差异造成的。320~330nm波长范围内，4μs延迟结果和实验值符合较好，2μs延迟的计算值略小于实验值，原因和前述相同。

图  10  2μs和4μs延迟的辐射强度计算结果和对比

Fig.  10  Comparison of radiance between computation and experiment at 2μs and 4μs time delay

下载: 全尺寸图片 幻灯片

3   结论

在激波管中开展了激波速度5.70和6.20km/s的氮气环境气体辐射强度定量测试实验，进行了相应的非平衡流动与气体辐射数值计算，通过定量分析和对比，得到以下结论：

(1) 基于原位标定方法，建立了适用于激波管气体光谱辐射强度高分辨率高精度定量化测试的实验手段。开展的实验研究表明，该方法可靠，实验重复性较好，定量数据准确。

(2) 基于定量化测试技术，得到了不同激波速度下波后平衡区和非平衡区的气体光谱辐射强度定量分布。数值计算得到了对应激波速度和压力条件下的流场参数和气体辐射分布，结果与实验值符合很好，验证了数值模型和方法。对不同波速状态的计算和对比也表明，非平衡区内的辐射强度明显高于平衡区。

(3) 不同的激波速度条件下，计算结果与实验值在320~330nm附近均存在偏差，可能来自于测量误差，或计算用反应模型中离子化反应速率等常数的不准确，后续研究中应针对该现象，完善实验测试技术，提高测量精度，在提供准确数据的基础上改进化学反应模型。