0   引　言

在高超声速飞行条件下，湍流引起的壁面摩擦系数和热传导系数远大于层流，同时，边界层转捩位置变化也直接影响飞行器的摩擦阻力分布和流动分离位置等。边界层转捩过程受多种因素和物理机制影响，飞行器的外形、弹道和姿态不同，相应的转捩问题也不尽相同。经过半个多世纪研究，边界层转捩依然是流体力学长期关注但尚未解决的重要研究问题之一。开展高超声速边界层转捩研究对高超声速飞行器研制具有重要意义^[1]。

在超声速及高超声速边界层流动中，由自由来流扰动引起的自然转捩过程主要包含以下4类不稳定波：第一模态波^[2]、第二模态波^[3-4]、横流不稳定波^[5]、Görtler不稳定波^[6]。第一模态为涡波扰动，最不稳定的波是三维模态形式，通常在低马赫数超声速流动中占主导；第二模态为声波扰动，属于二维模态，通常在马赫数大于４以后逐渐占据主导地位；横流不稳定波包括定常和非定常2种形式，主要发生在出现横流的流场中（如有迎角圆锥、后掠翼等情况下），定常横流不稳定波由壁面粗糙度引起，非定常横流不稳定波由自由流扰动引起；Görtler不稳定波主要发生在内凹曲面（如冲压发动机前体等^[7]）边界层中。

钝头圆锥形状具有一般轴对称飞行器的几何特征，是高超声速边界层转捩研究的典型外形。受马赫数、雷诺数、头部钝度和迎角等影响，其边界层转捩过程会发生很大变化，从而显著影响飞行器的气动力/热特性与气动稳定性。对于圆锥体类的高超声速构型，引起边界层转捩的主要机理是横流和Mack第二模态不稳定性^[8]。在轴对称流动中，当来流马赫数超过4之后，第二模态扰动将逐渐占主导。但当边界层外缘马赫数小于7时，第一模态扰动仍对转捩有重要影响，重要程度与壁面冷却程度等因素有关^[9]。自Mack提出高阶扰动模态概念之后，高阶扰动模态测量成为高超声速边界层转捩研究的重要方向之一。目前，在高超声速风洞边界层转捩实验研究中，最常用的方法是通过热流测量技术对转捩的位置、状态加以判断分析，测量手段主要有热电偶、红外测热和温敏漆（Temperature Sensitive Paint, TSP）技术等。在稳定性研究中，最常用的方法是通过脉动压力测量获得第二模态波的扰动幅值和频率。

从20世纪60年代开始，国外针对圆锥外形开展了大量高超声速边界层转捩实验研究。Muir^[10]、Stetson^[11]、Juliano和Willems^[12-14]等分别对不同半锥角模型开展了边界层特性测量实验，获得了丰富的转捩位置和边界层不稳定性数据。Stetson等^[15]采用高速热线风速仪对马赫数8、半锥角7°尖锥模型开展了详细的边界层稳定性实验，测量了流向不同站位上不稳定波的频率、振幅、增长率等，发现边界层内扰动主要体现为压力和温度脉动，而速度脉动相对较小，边界层内第二模态增长率远高于其他模态，是最不稳定波。近年来，Juliano等^{[12, 14]} 采用红外测热和高频压力传感器等测量手段，在H2K风洞上开展了圆锥模型边界层转捩实验，在来流马赫数7下研究了来流雷诺数和头部钝度变化对边界层转捩的影响规律。Casper等^[16]在Sandia高超声速风洞和Boeing/AFOSR 静风洞上针对半锥角7°尖锥模型开展了马赫数5、6、8和14的边界层转捩实验，采用了高速纹影、Kulite Mic–062压力传感器、PCB132型压力传感器和Medtherm型同轴热电偶等测量手段，实验结果表明马赫数5的边界层转捩是由第一和第二模态共同作用引起的。

张传鸿等^[17-18]在锥–裙模型稳定性实验中发现，边界层中第二模态不稳定波沿流向先逐渐增大而后快速消失，而第一模态波保持单调增长，直至转捩发生，由此他们认为是第一模态诱发了静音风洞条件下的转捩过程，而非通常认为的第二模态，该结论与之前类似风洞实验结果不同。常雨等^[19]在中国空气动力研究与发展中心（CARDC）的FD–14A激波风洞中，针对平板模型开展了高超声速边界层转捩实验研究，结果表明平板边界层的脉动压力系数与热流具有相同的变化趋势，并在马赫数8时捕捉到了第二模态扰动。刘小林和易仕和等^[20]在国防科技大学马赫数6静音风洞中采用平面激光散射（Nano–Tracer Planar Laser Scattering, NPLS）技术测量了锥裙边界层中的流动结构，给出了清晰的第二模态绳状结构和转捩后的湍流涡结构，获取了第二模态波的频谱特征，并测量到了一次和二次高频谐波。

国内在高超声速边界层转捩方面的研究起步较晚，尤其是风洞实验，在测试设备、测试技术、实验模型等方面，都与国外存在不小差距。目前国内还缺乏系统、完整的流动参数规律研究，难以为转捩理论验证、转捩模型构造和转捩控制等提供基础数据库和技术支撑。因此，在国家重点研究计划“大科学装置前沿研究”重点专项“高超声速边界层转捩机理、预测及控制方法研究”项目支持下，本文在CARDC的Φ1 m高超声速风洞上开展半锥角7°尖锥模型高超声速边界层转捩实验研究。前期已开展了基于非金属模型的红外测温实验^[21]，获取了雷诺数、马赫数对边界层转捩位置的影响规律。在此基础上，本文采用PCB高频脉动压力传感器进行不稳定波测量实验，结合线性稳定性分析工具^[22]研究马赫数、雷诺数对高超声速边界层转捩过程中不稳定波的影响规律及导致转捩的流动机制。

1   实验设备及测试仪器

1.1   风洞

实验在CARDC的Φ1 m高超声速风洞马赫数4～8支路上进行，如图1所示。该风洞是一座暂冲吹吸式常规高超声速风洞^[21]。

图  1  Φ1 m高超声速风洞

Fig.  1  Φ1 m hypersonic wind tunnel

下载: 全尺寸图片 幻灯片

1.2   测试仪器

1.2.1   PCB高频脉动压力传感器

高超声速边界层转捩过程伴随高频扰动的产生，即第二模态扰动波出现，频率高达数百千赫兹量级，且高频扰动占主导地位。高频扰动特性（频率、幅值等）会随着转捩的发生、发展，发生相应改变。

高频脉动压力信号测量要求压力传感器具有快速响应、高灵敏度、高固有频率等特性。PCB高频脉动压力传感器的固有频率可达10³ kHz、下限截止频率11 kHz，在国外已广泛应用于高超声速边界层失稳频率测量。最早由日本富士公司在日本宇宙航空研究开发机构的0.5 m高超声速风洞（JAXA HWT1）中用于测量第二模态扰动，随后应用于波音/AFOSR马赫数6静音风洞。

本文采用PCB132A31型高频脉动压力传感器，传感器通过专用信号调理器和线缆连接到风洞高精度动态数据采集系统，脉动压力采样频率3 MHz。

传感器技术指标为：直径3.18 mm；谐振频率大于1 MHz；最小测量压力7 Pa；最大压力5516 kPa；使用温度范围–18～79 ℃。

每次吹风实验有效测量时间为2 s，采样频率为3 MHz。功率谱密度计算时长为0.8 s，分为512个样本长度，相邻2个样本重叠50%，计算结果的频率分辨率为2.9 kHz。

2   实验模型及实验状态

风洞实验模型为7°半锥角尖锥（图2），理论长度L = 800 mm，底部直径D = 196.46 mm，头部半径R_n = 0.05 mm，表面粗糙度1.6 μm。模型分为2段，由不同材料加工：头锥段为金属，后锥体为聚四氟乙烯。沿锥模型子午线（0°）安装了8个PCB脉动压力传感器，第一个传感器轴线与模型子午线交点到模型理论尖点的距离l = 125 mm，各传感器间距80 mm，传感器位置见表1。模型采用尾支撑，通过快速送进机构从流场外迅速投放到流场中心。

图  2  实验模型

Fig.  2  Test model

下载: 全尺寸图片 幻灯片

表  1  PCB传感器安装位置

Table  1  PCB installation locations

PCB 编号	1	2	3	4	5	6	7	8
l/mm	125	205	285	365	445	525	605	685

下载: 导出CSV 

| 显示表格

在常规高超风洞条件下，研究了马赫数、雷诺数对高超声速边界层转捩的影响规律和边界层转捩特性。雷诺数和马赫数影响规律在0°迎角（实际迎角为0° ± 0.1°）下开展，自由流马赫数5～8，单位雷诺数Re_∞ = 0.49 × 10⁷～2.45 × 10⁷ m^–1。风洞实验流场参数及风洞来流噪声水平详见参考文献[21]。

3   实验结果

3.1   基本状态

实验参数设置为：来流马赫数6，单位雷诺数Re_∞ = 1.00 × 10⁷ m^–1，头部半径R_n = 0.05 mm。

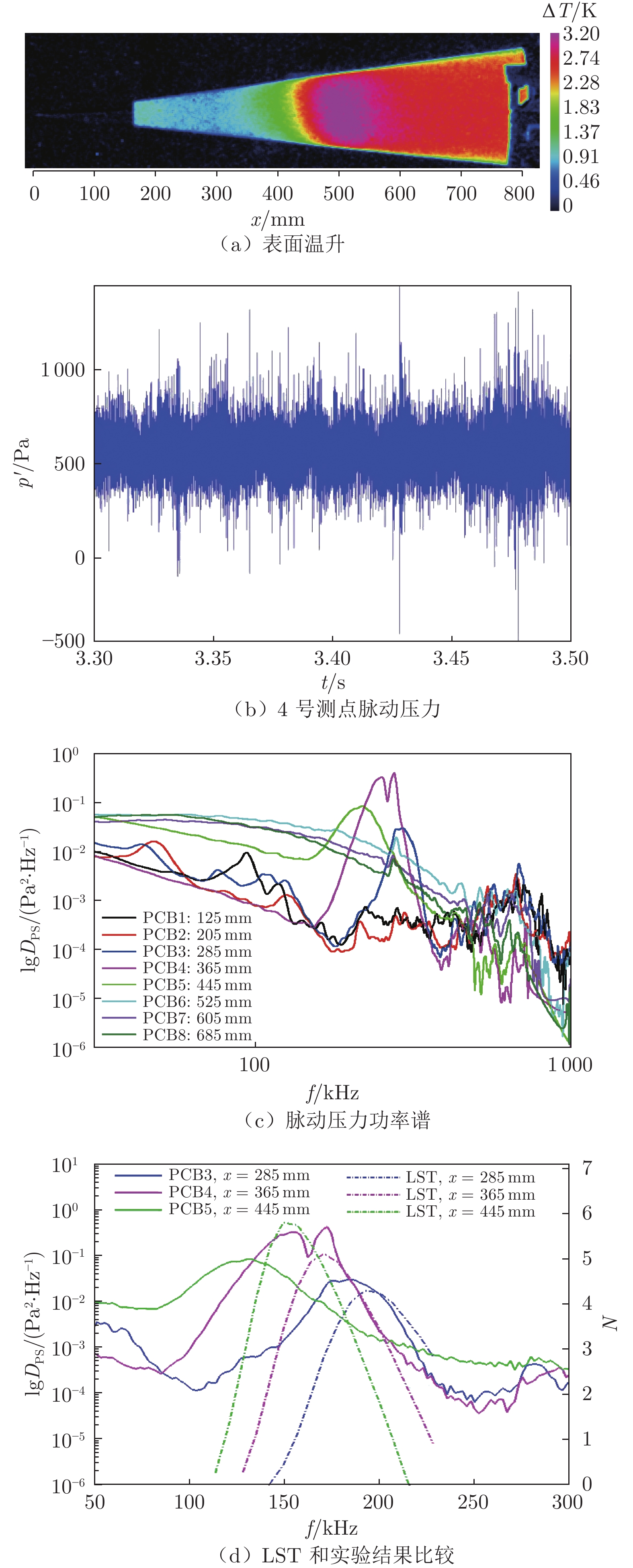
图3（a）为模型表面温升ΔT分布，通过比较温度变化可判断转捩发生情况，图中x = 0和800 mm分别为模型理论尖点和底部位置。中心线温升最低点和最高点分别位于x = 300和500 mm处，说明中心线转捩起始点和结束点在x = 300和500 mm处。

图  3  模型表面温升分布和脉动压力功率谱 （Re_∞ = 1.00 × 10⁷ m^–1）

Fig.  3  The temperature rise distribution and fluctuating pressure power spectrum of the model surface（Re_∞ = 1.00 × 10⁷ m^–1）

下载: 全尺寸图片 幻灯片

图3（b）给出了4号测点脉动压力p' 随时间t的变化规律。图3（c）给出了模型表面沿流向8个测点的脉动压力功率谱（D_PS）。在低频段（频率f < 110 kHz），前3个测点表现出一些较小峰值，可能由风洞噪声或其他原因导致；而多数测点在500 kHz以上没有表现出明显的规律，推测是由风洞噪声或系统测量误差导致，风洞噪声水平详见参考文献[21]。下面主要针对中间频段有明显峰值信号的数据进行分析。

从图3（c）中可以看到，3号测点处于转捩起始点前，出现了一个显著的脉动压力功率谱峰值，其中心频率290 kHz。随着向下游发展，边界层变厚，脉动压力功率谱峰值增大，但频率减小。4号测点处出现最大脉动压力扰动，频率为270 kHz。5号测点处压力脉动峰值减小，且低频段幅值上升数倍，推测由大扰动破碎导致。

图3（d）给出了3、4、5号测点通过线性稳定性分析（LST）得到的第二模态不稳定波增长因子N。在3号和4号测点处，LST得到的第二模态主频分别为302和269 kHz，和实验测量主频十分接近，偏差在5%以内，说明这2个测点测量的不稳定波属于第二模态波。在5号测点处，实验测量的峰值频率明显低于稳定性分析值，二者相差10%，且测量的波峰包含频率明显更宽，主要原因是该测点处的转捩处于转捩后期，边界层中的扰动波经过线性增长后进入非线性增长阶段，多种扰动成分对压力脉动信号都有贡献，形成宽频功率谱峰。在400～700 kHz区间，尽管幅值较小但仍可分辨出3号和4号传感器测量的峰值，初步判断为第二模态的高频谐波。

在6号测点及下游更远的7号和8号测点处，脉动压力功率谱峰值消失（图 3（c）），在更宽的频率范围内存在更多的功率，说明边界层已完全处于湍流状态。

3.2   雷诺数影响规律

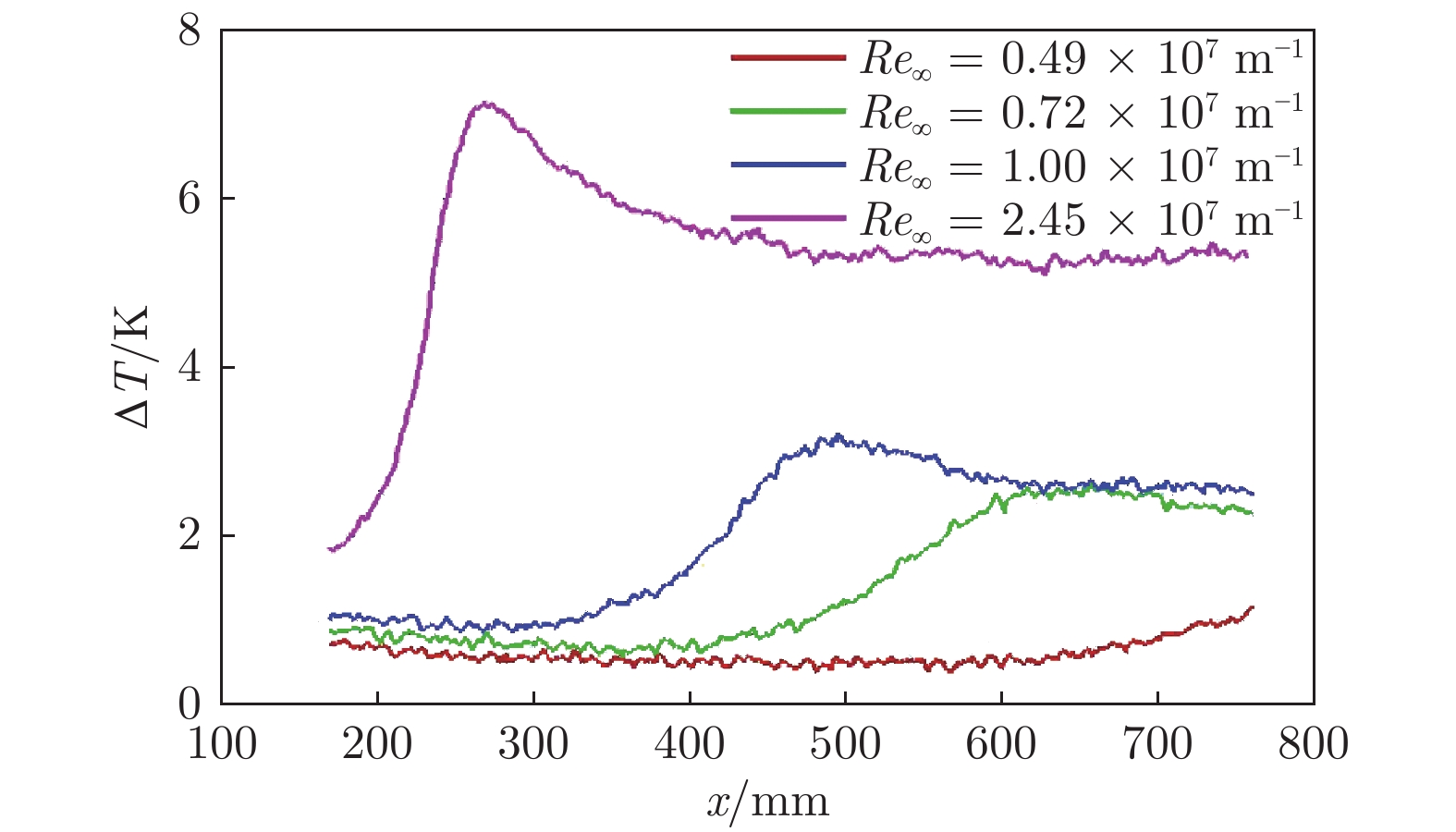
以Re_∞ = 1.00 × 10⁷ m^–1为基础，开展雷诺数影响实验（Re_∞ = 0.49 × 10⁷、0.72 × 10⁷、2.45 × 10⁷ m^–1）。来流马赫数为6，通过调节风洞来流总压调节雷诺数。图4和5给出了4个雷诺数条件下的模型表面温升分布。观察转捩起始和结束位置可以发现，随着雷诺数增大，转捩位置逐渐前移，转捩过渡区域缩短。转捩位置不完全对称，主要是由模型加工和安装偏差、风洞流场非绝对均匀等原因所导致。

图  4  模型表面温升沿子午线变化曲线

Fig.  4  Surface temperature rise of centre lines on model surface

下载: 全尺寸图片 幻灯片

图  5  模型表面温升分布

Fig.  5  Surface temperature rise on model surface

下载: 全尺寸图片 幻灯片

当Re_∞ = 0.49 × 10⁷ m^–1时，转捩起始点位于x = 600 mm处，在模型底部（x = 800 mm）转捩过程仍未完成。图6（a）为8个PCB测点的脉动压力功率谱。与Re_∞ = 1.00 × 10⁷ m^–1类似，在6～8号测点上出现了3个明显的功率谱峰值，6号测点处峰值频率约为144.2 kHz。随着向下游发展，峰值频率降低，宽度增大，幅值增大。7号和8号测点处于转捩发生的起始阶段，扰动波幅值逐渐增大。8号测点处功率谱峰值频率为121.2 kHz。在8号测点处边界层转捩尚未完成，扰动仍在增长，没有探测到功率谱峰值减小的过程。

图  6  脉动压力功率谱和线性稳定性分析 （Re_∞ = 0.49 × 10⁷ m^–1）

Fig.  6  Fluctuating pressure power spectra and linear stability analysis （Re_∞ = 0.49 × 10⁷ m^–1）

下载: 全尺寸图片 幻灯片

图6（b）将稳定性分析的最不稳定第二模态波增长因子N和测量的脉动压力功率谱结果进行对比。在6、7、8号测点处，脉动压力功率谱峰值频率和第二模态主频十分吻合，吻合程度好于Re_∞ = 1.00 × 10⁷ m^–1的情况，说明低雷诺数下边界层扰动更趋于线性增长。与Re_∞ = 1.00 × 10⁷ m^–1条件下的功率谱不同，3个测点脉动压力功率谱在200～300 kHz区间出现了峰值，尽管幅值较小，且受背景噪声干扰出现锯齿形波动，但可以判断为第二模态的高频谐波，其频率约为基频的2倍。

当Re_∞ = 0.72 × 10⁷ m^–1时，转捩起始点位于x = 420 mm处，结束点位于x = 620 mm处。如图7所示，在4号测点处，出现了高于基线量级的脉动压力功率谱峰值，中心频率为222 kHz。随着边界层变厚，脉动压力功率谱峰值逐渐增大，频率减小。功率谱最大峰值出现在6号测点处，频率为180.5 kHz。在7号和8号测点等更远的下游处，由于第二模态波破裂，边界层变成全湍流，功率谱峰值降低，但在更宽的频率范围内存在更多的功率。线性稳定性分析给出了4～7号测点处第二模态不稳定波N值分布，主频和PCB测量结果接近。另外，在当前工况下没有观测到高频谐波。

图  7  脉动压力功率谱和线性稳定性分析 （Re_∞ = 0.72 × 10⁷ m^–1）

Fig.  7  Fluctuating pressure power spectra and linear stability analysis （Re_∞ = 0.72 × 10⁷ m^–1）

下载: 全尺寸图片 幻灯片

当Re_∞ = 1.0 × 10⁷ m^–1时，在3号测点处开始出现高于基线量级的脉动压力功率谱峰值，下游4号和5号测点也有明显的峰值，主频与线性稳定性分析的第二模态接近。从6号测点开始，边界层转捩过程结束，处于湍流状态，没有功率谱峰值，但在更宽的频率范围内存在更多的功率，详见3.1节，这里不再赘述。

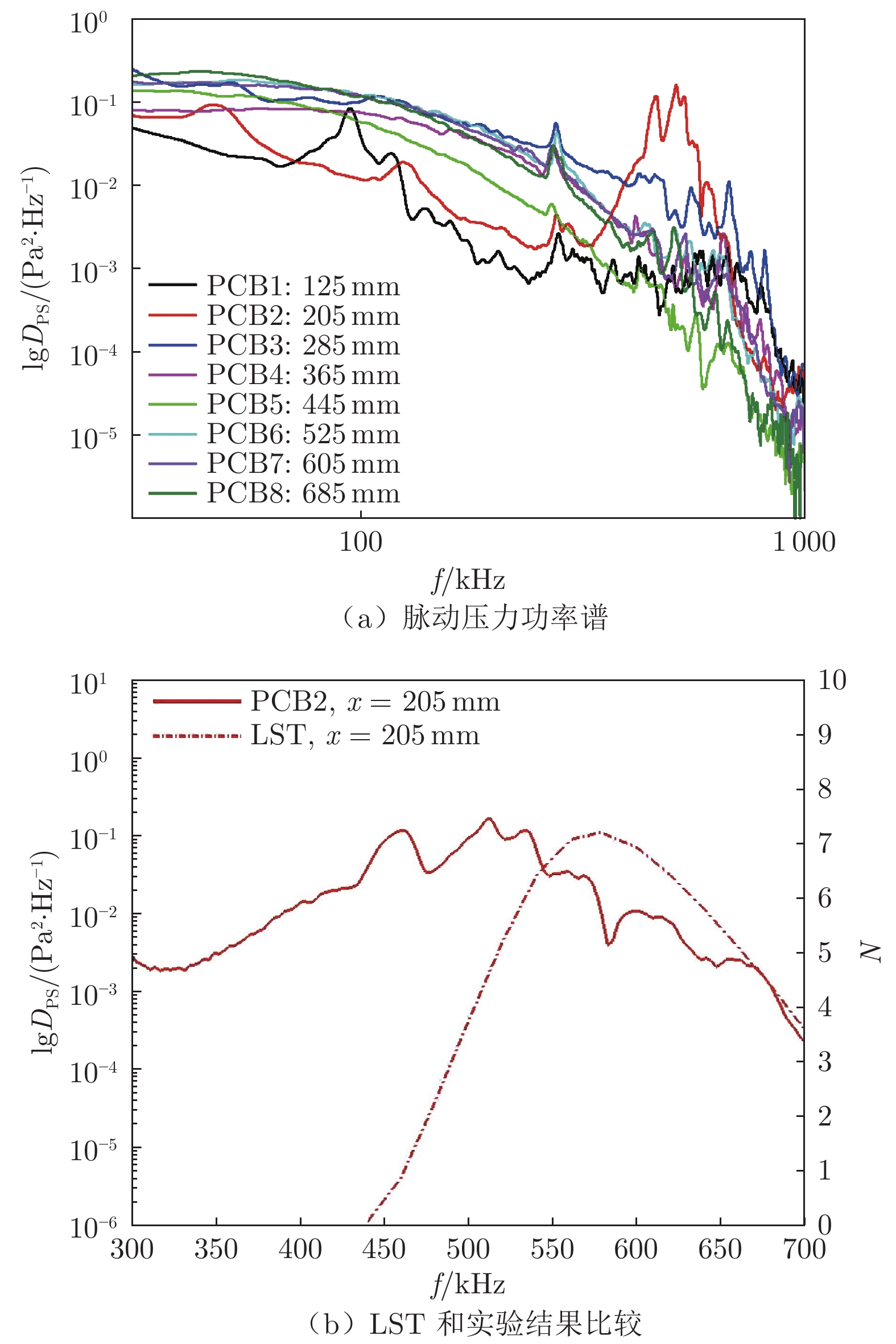
随着单位雷诺数进一步增大，当Re_∞ = 2.45 × 10⁷ m^–1时，壁面温升起始点更加靠前，由于模型头部（${{x}}\leqslant165\;{\rm{mm}}$）是金属材料，不能获得红外热图测量结果，因此转捩起始点位置可能比x = 165 mm处更靠前，但根据图4可判断转捩结束于x = 270 mm处。图8（a）给出了8个PCB测点的测量结果。在2号测点处出现了功率谱峰值，频率为505.5 kHz。从3号测点开始，没有出现明显功率谱峰值，功率在更宽频率范围内分布，印证了此时的边界层已经是完全湍流状态。图8（b）对2号测点进行了稳定性分析，该位置存在增长的第二模态，但主频高于实验测量值。

图  8  脉动压力功率谱和线性稳定性分析（Re_∞ = 2.45 × 10⁷ m^–1）

Fig.  8  Fluctuating pressure power spectra and linear stability analysis （Re_∞ = 2.45 × 10⁷ m^–1）

下载: 全尺寸图片 幻灯片

脉动压力测量结果表明，随着Re_∞从0.49 × 10⁷ m^–1增大到2.45 × 10⁷ m^–1，转捩位置逐步向上游移动，边界层中最早出现功率谱峰值的位置也随之向上游移动，相同位置的脉动压力功率谱峰值逐渐增大，频率增大。雷诺数增大使得第二模态不稳定波更早地出现，导致转捩提前。

3.3   不同来流马赫数实验

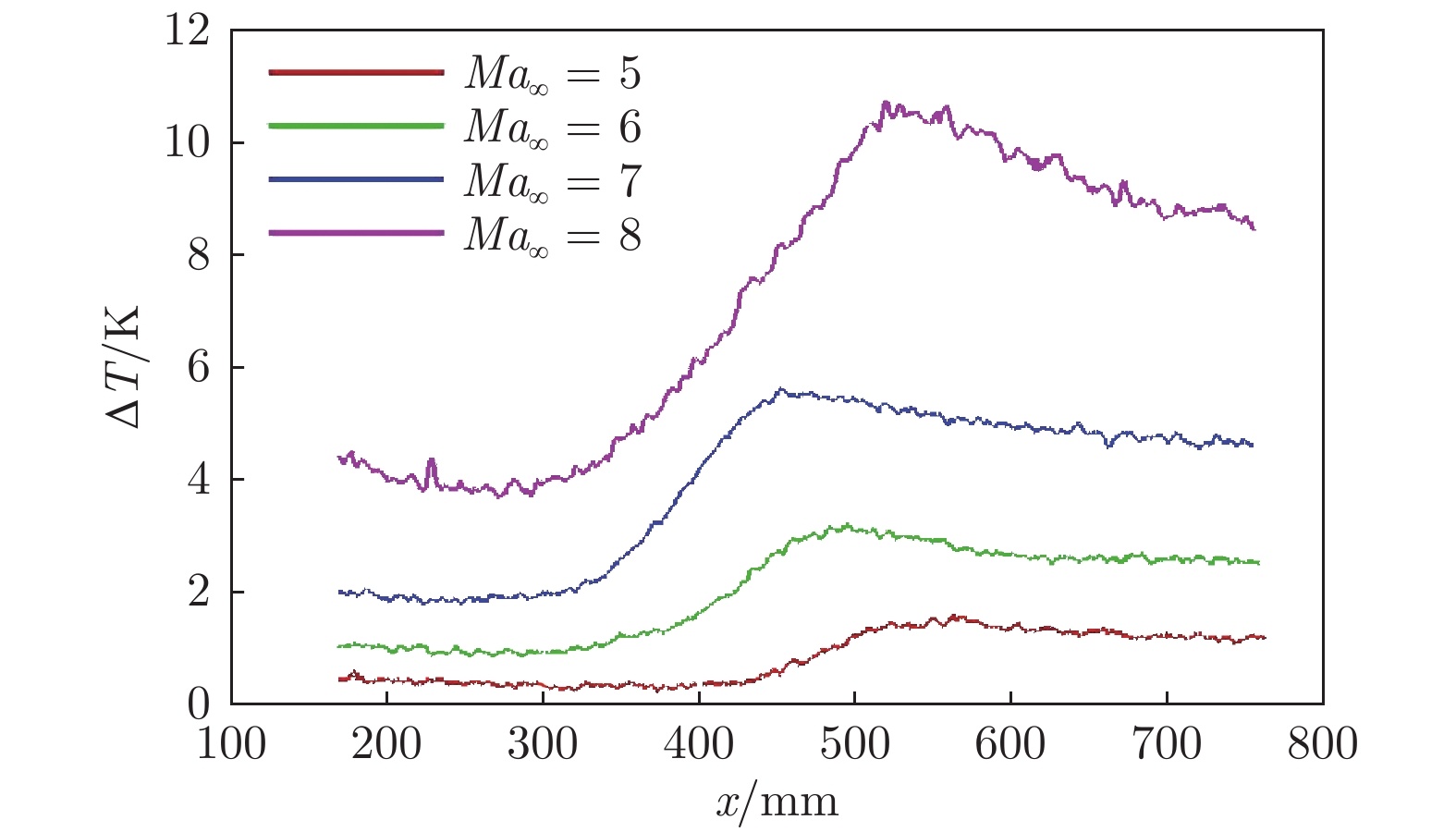
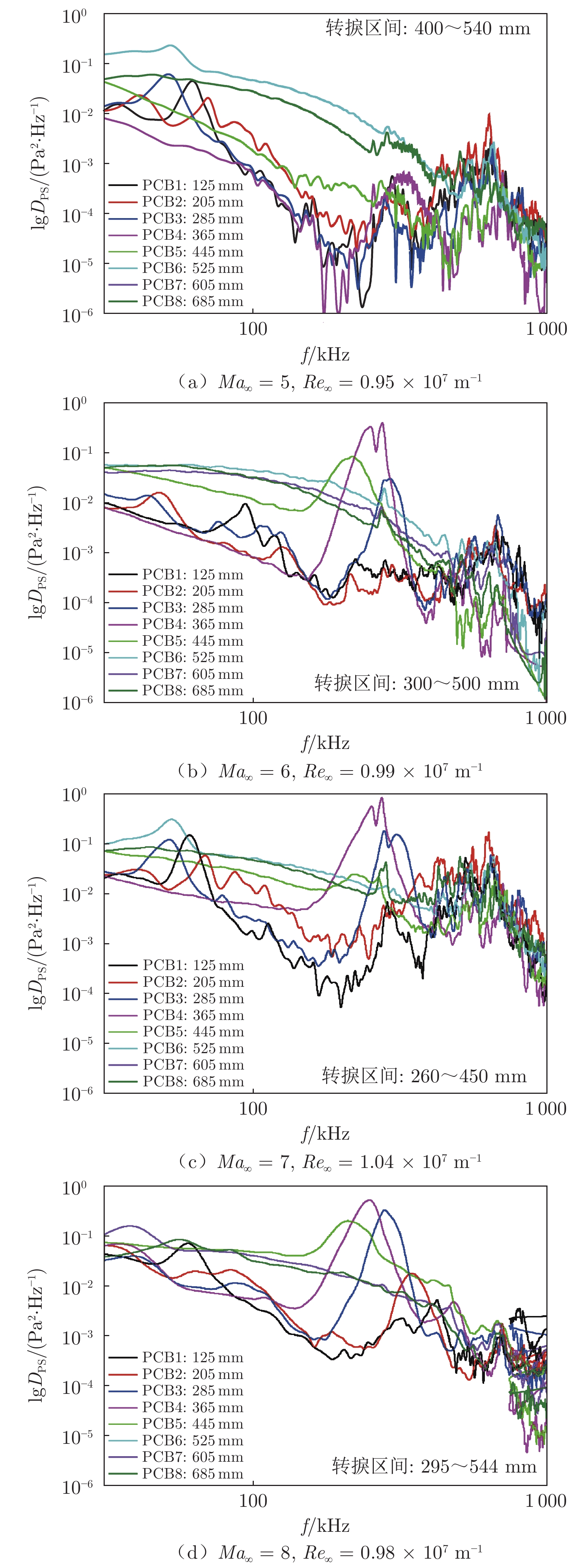
针对来流Re_∞ = 1.0 × 10⁷ m^–1，进行了马赫数Ma_∞ = 5、6、7、8等4个工况下的边界层不稳定波测量，结合LST结果对边界层不稳定波特性进行了分析。图9和10给出了4个马赫数条件下的模型表面温升变化^[21]。可以看到，对应于马赫数5、6、7、8，转捩起始点依次为x = 400、300、260和295 mm，先前移再后移，转捩过渡区则有逐渐变长的趋势。马赫数的影响规律并不符合马赫数增大会使转捩位置后移的认识，这主要是由不同马赫数条件下风洞实际单位雷诺数和自由流噪声水平差异所导致。

图  9  模型表面温升沿子午线变化曲线

Fig.  9  Surface temperature rise of centre lines on model surface

下载: 全尺寸图片 幻灯片

图  10  模型表面温升分布

Fig.  10  Surface temperature rise on model surface

下载: 全尺寸图片 幻灯片

图11为不同Ma_∞时脉动压力测量结果。由于传感器接线故障，Ma_∞ = 5和7时的7号测点、Ma_∞ = 8时的6号测点未探测到有效数据。在Ma_∞ = 5时，从红外测量结果上看，模型表面出现了转捩，但在8个脉动压力传感器测量结果中（图11（a））并没有发现明显的第二模态波功率谱峰值，4号测点在320 kHz附近存在一个较弱的峰值，其最大D_PS值的对数约为6 × 10^–4，比3.2节中边界层内第二模态的幅值低约2个量级，推测该扰动不是导致Ma_∞ = 5时流动转捩的主要不稳定波。1～3号测点的PCB测量结果中出现的低频峰值（在其他马赫数时也存在），目前还难以确定其来源。

图  11  模型表面脉动压力功率谱

Fig.  11  Fluctuating pressure power spectra on model surface

下载: 全尺寸图片 幻灯片

图11（b）为Ma_∞ = 6时的脉动压力功率谱，可以看到从3号测点开始出现明显的大幅值扰动波，前文分析也说明该处扰动属于第二模态，不再赘述。

图11（c）为Ma_∞ = 7的脉动压力测量结果，与Ma_∞ = 6情况类似，在3号和4号测点处出现大幅值扰动，其主频分别为300和270 kHz，略高于Ma_∞ = 6的情况，可能是由于实验雷诺数略高所导致。5号测点处于转捩区末端，第二模态扰动主频已不甚明显，但仍然存在一个较小峰值。

图11（d）为Ma_∞ = 8的脉动压力测量结果。相比其他马赫数工况，该流动条件下的第二模态主频更加明显。最早在2号测点处观察到342 kHz主频的扰动，3、4、5号测点对应的主频分别为280、245、210 kHz。4号测点出现明显的第二模态的高频一次、二次谐波，主频分别为490、735 kHz。

Ma_∞ = 6、7、8的尖锥脉动压力测量结果基本类似，都在转捩区结束前出现较大幅值的第二模态不稳定波，频率也较接近。Ma_∞ = 8时第二模态频率低于Ma_∞ = 7，与其边界层增厚有关。而Ma_∞ = 5时尽管有转捩发生，但是没有测到类似的第二模态脉动压力峰值信号，为此针对Ma_∞ = 5和6状态开展了稳定性分析。

图12给出了Ma_∞ = 5和6时流场的第一模态和第二模态N值分布，第一模态分析的频率范围为30～110 kHz，第二模态分析的频率范围为150～360 kHz。可以看到：Ma_∞ = 5时，第一模态的N值远高于第二模态，说明第一模态的扰动占主导；而Ma_∞ = 6时，第二模态的N值明显高于第一模态的N值，说明第二模态的扰动占主导，在实际的脉动压力测量中也更容易观察到第二模态功率谱峰值。

图  12  第一模态、第二模态的N值分布

Fig.  12  N-factors of first-mode and second-mode disturbance

下载: 全尺寸图片 幻灯片

因此，Ma_∞ = 5的边界层转捩是由第一模态作用引起的，而对于更高的马赫数，在湍流斑点出现之前，边界层主要由第二模态主导。这与Casper等^[16]在Sandia高超声速风洞中得到的实验结果类似：他们在尖锥Ma_∞ = 5流场的高速纹影图中观察到了低频和高频扰动波，其频率分别对应第一和第二模态，由此得出转捩是由2种模态共同作用导致的结论。但本文通过稳定性分析发现，第一模态的增长率高于第二模态，而且PCB传感器没有测量到明显的第二模态特征信号，因此推断Ma_∞ = 5实验中的边界层转捩主要由第一模态导致。

Ma_∞ = 5时转捩起始位置（x = 400 mm）对应的第一模态N值约为6，Ma_∞ = 6时转捩起始位置（x = 300 mm）对应的第二模态N值约为5，说明第二模态的初始幅值高于第一模态，这也符合高超声速风洞流场以声波扰动为主的噪声特征。

4   结　论

在Φ1 m高超声速风洞中，针对7°半锥角尖锥模型开展了边界层转捩实验研究，结合前期红外热图测量结果，采用高频脉动压力测量技术分析了马赫数、单位雷诺数等对尖锥边界层转捩过程中不稳定波的影响，结论如下：

1）随着边界层向下游发展，在第二模态波破裂前，扰动逐渐增大，脉动压力功率谱峰值逐渐增大；边界层逐渐变厚，第二模态波扰动频率逐渐减小。

2）随着雷诺数增大，转捩起始位置前移，转捩区缩短；第二模态波不稳定性增长提前，功率谱峰值最大值向上游移动；雷诺数增大使得边界层厚度减小，导致第二模态波的扰动频率向高频移动。

3）随着马赫数增大，边界层转捩的主导模态发生改变，转捩位置先前移再后移；马赫数5时，第一模态的增长因子明显高于第二模态，第一模态的扰动占主导，在更高马赫数时，第二模态的增长因子明显高于第一模态，第二模态的扰动占主导。

致谢：天津大学赵磊博士和空气动力学国家重点实验室陈曦博士在本文的稳定性分析中给予了大力支持和帮助，特此表示衷心感谢。