Simulating hypersonic projectile launching process in the ballistic range by Adaptive Discontinuity Fitting solver technique
-
摘要: 弹道靶自由飞试验是高超声速领域中的一种重要的地面试验手段。试验中厘米级的弹丸/弹托在10米级长度的管道中加速至极高的速度，出膛后通常采用气动力使弹托偏离预定弹道而被拦截器阻挡，仅使弹丸进入试验段开展测试。由于发射过程中弹丸的实际飞行姿态会受到管道内长距离加速、高压驱动下出膛、气动分离干扰等诸多因素的影响，因此基于计算流体力学发展相关的气动预测技术有助于指导试验方案设计，从而保证弹丸运动轨迹的准确性。针对发射问题中涉及的诸如空间尺度变化剧烈、接触-分离、超高速动态分离等数值仿真难点，采用基于非结构动网格技术和格心型有限体积方法发展的自适应间断装配求解器（ADFs），对非定常流场中的运动激波进行装配，通过二维算例对弹丸发射过程数值仿真进行了详细的原理性介绍。一方面，拓展了激波装配方法在工程问题中的应用；另一方面，针对弹道靶中超高速弹丸发射这类问题，建立了一套高效的数值模拟方法，实现了对弹丸从静止到加速、出膛、分离的全动态过程的精细流场刻画。Abstract: The free flight ballistic range is an important ground test method for the study of hypersonic vehicles. After the accelerated launch, the projectile is separated from the sabots in the range tank. The actual flying posture of the projectile is affected by many factors occurring in the processes of model acceleration and separation. Therefore, it is helpful to operate the experiment by developing simulation techniques for ballistic range tests. Considering the above processes, a set of numerical simulation algorithms is built. More specifically, the unstructured dynamic grid technique and Adaptive Discontinuity Fitting solver(ADFs) are used to track the motion of the projectile and sabots, and the cell-centered finite volume method is utilized to update the flow field.
-
Keywords:
- ballistic range /
- numerical simulation /
- multi-bodies separation /
- hypersonic /
- shock-fitting
-
0 引言
超声速自由飞弹道靶是专门用于炮弹、火箭、导弹或其他飞行器模型的自由飞试验、进行气动力和弹道性能研究的封闭式射击靶道[1]，是现代气动试验最重要的设备之一。模型发射装置是弹道靶的重要组成部分。当前使用最广泛的模型发射装置是二级轻气炮，其工作原理是利用火药爆炸对泵室内的轻气(如氢气或氦气)进行加温加压，驱动模型(弹丸与弹托)在较长的发射管中加速到极高的速度(如5km/s)[2]。
利用弹道靶发射弹丸时，必须借助弹托分离技术[3]。通常将弹丸固定在用塑料制成的弹托内，弹托外径与发射管内径相同；加速过程中，弹托与发射管接触摩擦；出膛后，利用气动力分离技术使弹托逐渐偏离预定弹道并被拦截器阻挡，仅使弹丸进入试验段开展测试。
当前，国内面向弹道靶开展的数值研究主要集中于运用经典内弹道理论以及计算流体力学(CFD)方法对二级轻气炮开展相关研究，为优化二级轻气炮性能提供可靠的数值分析手段[4-6]。弹丸从静止启动到加速、出膛、分离的过程，涉及的物理过程复杂、空间尺度差异较大、非定常效应明显、激波强度较高，对数值模拟提出了一定挑战，调研发现相关研究国内鲜有报道。
弹道靶中弹丸发射全过程存在强烈的气动干扰，强激波、膛口波系、高速膨胀气体都会对弹丸飞行运动造成比较大的影响。发展弹丸发射全过程数值模拟技术有助于弹道靶试验设计，以保证弹丸运动轨迹的准确性，避免出现弹丸偏离预定弹道而被拦截或打到靶室洞壁的情况。
本文采用刘君[7-8]等基于非结构动网格技术和格心型有限体积方法发展的自适应间断装配求解器(Adaptive Discontinuity Fitting solver，ADFs)对非定常流场中的运动激波进行装配，通过二维算例对弹丸发射全过程开展数值仿真，较为详细地介绍各个运动阶段数值模拟的特点。
1 计算方法
1.1 控制方程
计算主要考虑激波的影响，未考虑粘性效应。控制方程采用基于ALE(Arbitrary Lagrange-Euler)方法的可压缩非定常Euler方程的积分形式：
(1) 式中，Q为守恒变量，Fc为对流项通量，xc为网格运动速度，Ω、∂Ω分别为控制体和控制边界，n为控制体边界外法向向量，dV、dS分别为体积微元和面积微元。
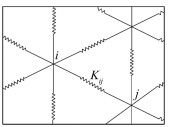
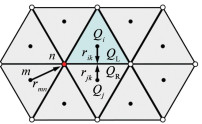
使用格心型有限体积方法时，流动变量存储在计算网格单元的中心。根据单元界面两侧的参数，通过通量矢量分裂方法计算对流项通量Fc，如图 1所示。若使用左右单元的格心值代表界面两侧的参数，则空间精度仅有一阶。为获得二阶精度，使用Gauss-Green公式计算单元梯度[9]：
(2) 其中，k遍历第i个控制单元的Nf个面元，Vi为控制体体积，Sk为第k个面元的面积，nk是面元单位外法向向量。网格节点上的流动变量
(3) 其中，Np为第k个面元所包含的节点数，Nc是与第n个网格节点相邻的单元的总数，cm是第m个邻居单元的距离反比权系数，即cm=1/|rmn|。
1.2 非结构动网格技术
高速条件下的多体分离流场呈现高度非线性和非定常的特征。对此类问题进行数值模拟，按照依赖网格技术的差异主要分为3种方法，即动态嵌套网格[10-11]、非结构动网格[12-13]和笛卡尔自适应网格[14-15]。本文使用基于顶点模型弹簧近似法的非结构动网格技术[16]，下面对该技术进行简要介绍。
如图 2所示，弹簧近似法将网格单元的每条边视作弹簧，认为网格点i和j之间的弹簧张力与两节点之间距离成正比，满足Hooke定律。因此，对作用于节点i的所有弹性力进行合成，可得：
(4) 其中，Ni是与节点i相连的节点总数，Kij是网格边ij的弹簧倔强系数。
根据初始时刻的网格，按照上式可以得到初始状态下每个网格点i受到的合力。当某些节点移动后，弹簧长度变化使得该点的受力发生变化，为了保持整体受力平衡，需要调整其他网格点的位置。由于网格变形过程中每点的合力不变，新的网格分布依然满足上式。
1.3 激波装配技术
对于含有强激波的流动问题，若单纯使用捕捉方法进行处理，会存在数值不稳定问题，同时也会影响流场的计算精度[17]。计算激波一个最直接的办法就是使用激波装配方法，即将激波面看作一个间断，使两侧的物理量在激波法向上满足Rankine-Hugoniot(R-H)公式：
(5) 式中，ρ1和ρ2是激波上下游密度，u1和u2是激波上下游的流动速度，p1和p2是上下游压强，h1和h2是上下游比焓。
最早的激波装配方法可以追溯到20世纪40年代，经过半个多世纪的研究，特别是近十几年的发展，其实用性已有了明显提高[18]。刘君等人基于非结构动网格技术发展出的ADFs具有较强灵活性，能够很好地满足本文模拟非定常流动下强激波的需求。
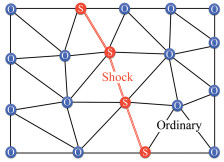
如图 3所示，在二维情况下，对于初始流场中预先给定的激波线，其上各个网格节点的属性可以在激波节点(S)和普通节点(O)之间灵活转换，自动适配当前流场状态；即，当实际激波尚未到达给定线时，该线不作为激波进行装配计算，仅当实际激波到达时，才转化为激波进行装配。在下文2.1节有相关具体阐述。
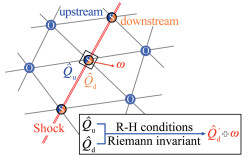
相对于定常计算，在非定常计算过程中，运动激波的装配无需进行特殊处理，这也是ADFs的一个优点。具体来讲，当推进到n+1时刻时，首先根据n时刻物理量通过R-H关系式迭代求解各个激波节点的运动速度ω(如图 4所示，对于定常计算收敛时，ω→0)，从而得到n+1时刻激波阵面位置；随后使用前文介绍的网格变形算法更新内部网格节点的位置，当网格变形较大时，需要进行网格重构；最后进行时间推进计算n+1时刻的物理量。也就是说，在原有的激波捕捉法求解器基础上，ADFs仅增加了一个装配激波的模块，通过输出激波节点参数(物理量及激波速度)和激波面元通量，建立了与捕捉法求解器的联系，故该算法很容易移植到任何含有动网格的程序中。限于篇幅，对ADFs的详细阐述请参阅文献[19]。
在空间离散上，采用目前流行的van Leer矢通量分裂格式，使用前文介绍的梯度重构方法，保证了空间离散具有二阶精度；时间推进采用显式四阶四步Runge-Kutta方法，时间步长的量级为10-6；使用商业软件POINTWISE划分全场网格，采用Advancing Front算法保证绝大部分区域网格为正三角形，提高了整体网格的质量。
2 数值仿真
在一些弹道靶试验中，通过点燃火药后形成的高温高压燃气驱动活塞对泵室内的气体加压；压力达到一定数值后，泵室和发射管之间的膜片破裂，高压气体直接作用于弹托底部，驱动弹丸/弹托一起加速运动；弹丸/弹托在比较长的发射管道中加速至预定速度，进入分离罐，在发射管出口的高压气体和弹丸/弹托附近的激波共同作用下，经过合理设计的弹托和弹丸可以实现气动力分离。
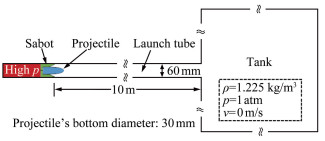
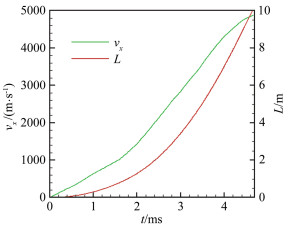
计算模型如图 5所示，主要包括发射管和分离罐两部分。发射管总长10m，管道内径0.06m；弹丸呈子弹头形，长0.10m，底部直径0.03m。弹丸在两个完全相同的弹托约束下沿着发射管水平向右方运动。根据文献[5]的数据，直接给定弹丸和弹托(后文也将弹丸和弹托合称为“模型”)在发射管内的加速过程，其沿x方向(发射管轴向)的运动速度vx和位移L的曲线如图 6所示。
![]()
图 5 弹道靶计算模型示意图Fig. 5 Schematic diagram of the computational model for ballistic range根据该问题的特点，整个试验过程可分为模型加速、激波出膛、模型出膛、气动分离4个阶段。
2.1 模型加速过程
该过程的一个显著特点是：物体的空间尺度相差较大，即与加速距离10m相比，模型尺寸要小若干个量级。如果直接对整体发射管进行建模，采用激波捕捉法求解模型沿发射管的运动，就会付出相当大的计算代价，对于三维问题而言尤其难以接受。
分析发现，模型加速运动会压缩处于上游的气体，使其头部某处形成一道向右运动的正激波，且激波阵面为模型加速运动形成的扰动的最远传递位置，而激波阵面上游流体则始终处于未扰动的静止状态。由于模型加速过程给定，可以不考虑其底部流动状态的变化，即在该过程中仅需计算激波和模型之间区域的流动变化。
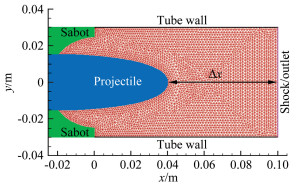
图 7给出了初始计算区域(x方向长约0.1m，占整个发射管长度的1/100；Δx为弹丸头部顶点与运动激波的水平距离)，以非结构三角形网格进行空间离散。设置模型右侧边界为激波边界，当激波未形成或激波未达到该位置时，使用ADFs可以切换激波边界为出口边界，不进行装配，此时计算网格随模型一起刚性运动，不发生变形；当激波形成且到达边界位置时，开始采用装配方法进行处理，激波边界条件启动。
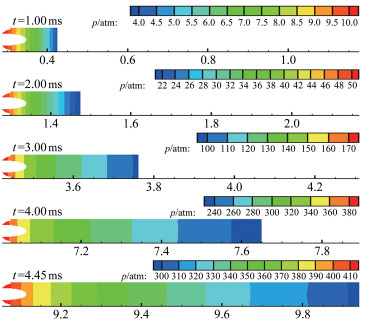
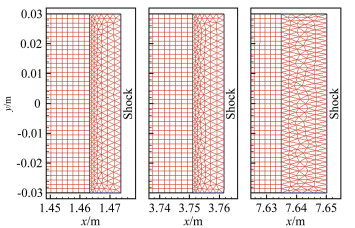
图 8给出了加速阶段5个时刻的压力云图。可以看出，由于激波运动速度大于模型运动速度，计算过程中计算区域会逐渐扩大。图 9给出了3个时刻激波附近的网格分布，自激波下游某处(图 9中四边形网格和三角形网格交界处)起至模型的这部分网格，可以设置为随模型一起运动的刚性运动网格，使全场网格变形及网格重构区仅包含激波附近若干层网格，从而提高全场网格质量，减少网格重构次数，极大地提高计算效率。
![]()
图 8 加速阶段不同时刻的压强云图Fig. 8 Pressure iso-contours at different moments in the accelerated process![]()
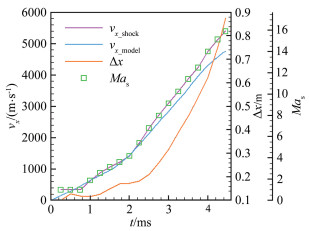
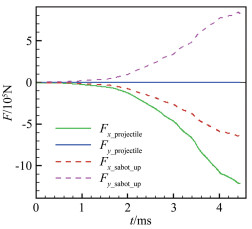
图 9 不同时刻激波附近的网格分布(从左至右：t=2.00ms, 3.00ms, 4.00ms)Fig. 9 Mesh distributions near the shock at different moments (from left to right: t=2.00ms, 3.00ms, 4.00ms)图 10为模型及激波的加速过程运动特性图(图中Mas为运动激波的马赫数)，图 11为弹丸和上弹托迎风面在加速阶段所受气动力F的变化曲线(Fx、Fy分别表示x、y方向的气动力)。在初始加速阶段，激波相对模型的运动速度较小，但加速度较高；在t=1.00ms时刻左右，激波运动速度超过模型运动速度；随后两者的速度差逐渐增大，激波强度逐渐增强，模型表面气动力开始快速升高；当模型运动加速度发生改变后(t=2.00ms)，激波的运动加速度也随之改变。因此，如果该过程的加速度曲线不同，即使模型到达发射管出口的速度一样，不同时刻的激波强度以及模型表面的压强也会有所差异。
![]()
图 11 加速过程弹丸和弹托的受力曲线Fig. 11 Aerodynamic force curves of projectile and sabots in the accelerated process值得注意的是：在模型加速过程中，激波前的相对马赫数会超过15，若在非结构网格中使用常规捕捉方法计算，很容易出现数值震荡，对计算方法的稳定性造成影响；而使用装配方法则能避免这个问题，这也是使用装配方法进行计算的另一个优点。
2.2 激波出膛过程
激波出膛过程从右行运动激波到达发射管口即将进入分离罐时刻开始计算，直到模型即将出膛终止计算。此阶段激波在分离罐中逐渐向前推进，最终形成了一个不断外扩的右行弧状激波阵面。此过程仍使用激波装配法处理该激波，计算区域随时间逐渐扩大。
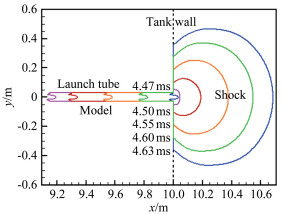
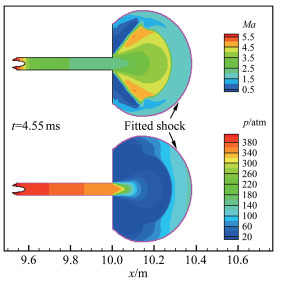
图 12给出了5个时刻激波阵面和模型的位置与形状变化，图 13为中间某时刻整个流场的压强与马赫数分布云图。计算初始时刻(t=4.47ms)，在发射管出口预设一个拟装配激波面，当激波未到达该位置时，流动按照捕捉方法进行计算；激波到达后，该界面逐渐全部变为激波阵面进行装配计算。
激波出膛之后，在分离罐壁面的作用下膨胀形成一个半圆形的影响区域。由于气流膨胀引起下游压强降低，靠近发射管轴线处的激波运动速度迅速降低，最终会小于模型运动速度；而在靠近壁面处，由于气流过膨胀，压力降幅更大，激波运动速度更小，最终造成靠近壁面的激波阵面向下游偏斜。
2.3 模型出膛过程
模型出膛过程涉及到动态多体分离中一个比较常见的问题——“接触-分离问题”。
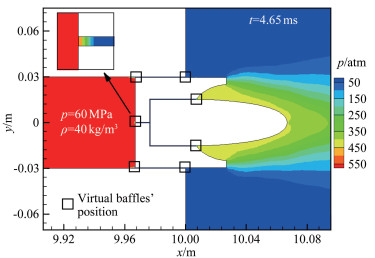
在发射出膛过程中，弹丸/弹托与弹托/发射管之间都保持接触状态，是一个典型的接触-分离问题。该过程存在网格拓扑变化，很难使用一套网格进行描述。处理此类问题，往往需要人为在物体之间设置一定缝隙。为尽可能减小缝隙对流动造成的影响，文献[20]发展出一种“虚拟网格通气”技术(如图 14所示)，在高压气体和缝隙的网格交界面设置“虚拟挡板”，防止弹丸/弹托上下游高压气体通过缝隙相互影响，物理上实现物体间的紧密接触状态。
![]()
图 14 模型出膛过程的“虚拟挡板”示意图Fig. 14 Schematic of virtual baffles in the process of themodel leaving the muzzle模型出膛后，其底部高压气体溢出，从而影响靶室内的流动状态。由于模型运动速度较快，相对时间尺度较小，为简化处理，假设发射管内高压气体的状态不变，即p=60MPa, ρ=40kg/m3。
2.4 气动分离过程
待完全飞出发射管，模型开始在气动力作用下进行六自由度运动。耦合求解流动方程和六自由度运动方程，获得流场以及模型位移和姿态的变化情况。在此过程中，可以使用前文介绍的非结构动网格技术描述模型运动轨迹。
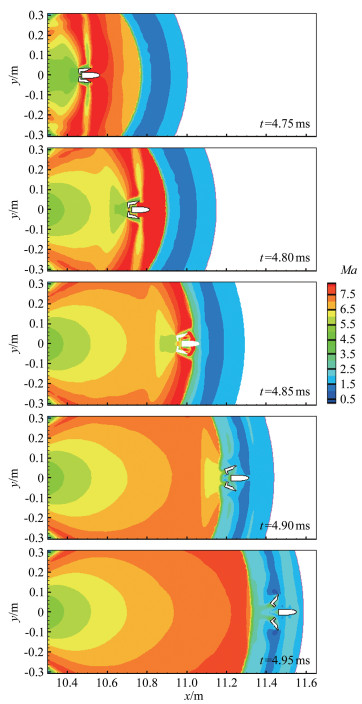
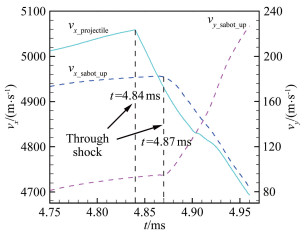
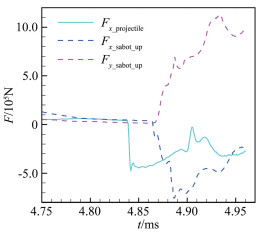
图 15为分离过程中5个时刻的马赫数云图，图 16、17分别为弹丸、弹托的速度vx以及气动力F的变化曲线。从云图中可以看出，在模型上游两道激波和尾部高速高压气流共同建立的流场下，模型逐渐追上前方两道激波。弹丸、弹托分别在t=4.84ms和4.87ms时刻开始穿过第一道内部膛口激波，进入激波下游高压区后，气动力急剧增大，x方向的运动速度逐渐降低。同时，由于弹托外形的不对称设计，其在y方向受到很大的气动力，迅速偏离弹丸的运动轨迹。在t=4.95ms时刻，弹丸即将追上并穿过初始右行弧状激波，从而摆脱该激波流场，进入试验段开展相关测试。
![]()
图 15 分离阶段不同时刻马赫数云图Fig. 15 Mach iso-contours at different moments in the process of sabot separation需要说明的是，虽然对发射过程开展二维模拟与实际情况不相符合，但是所得到的气动力可以定性地对这一过程的流动变化进行说明。
3 结论
将弹道靶试验中以超高速发射的弹丸作为研究对象，通过对二维问题的模拟，系统介绍了数值模拟时所需要的一些技术手段，如刚性和变形网格技术、虚拟网格通气技术、激波装配方法等。一方面，采用基于非结构动网格技术和格心型有限体积方法发展的自适应间断装配法，对该流场中大范围运动的高强度激波进行了装配计算，拓展了激波装配方法在工程问题中的应用；另一方面，针对弹道靶中超高速弹丸发射这类问题，建立了一套高效的数值模拟方法，实现了对弹丸从静止启动到加速、出膛、分离的全动态过程的精细流场刻画，有助于指导试验方案验证和优化设计。
一般而言，驱动段高压气体(如氢气)从发射管溢出后与空气相遇，还可能存在激波诱导燃烧等问题，因此，在下阶段工作中需要进一步考虑流动中的化学反应等。
-
![]()
图 5 弹道靶计算模型示意图
Fig. 5 Schematic diagram of the computational model for ballistic range
![]()
图 8 加速阶段不同时刻的压强云图
Fig. 8 Pressure iso-contours at different moments in the accelerated process
![]()
图 9 不同时刻激波附近的网格分布(从左至右：t=2.00ms, 3.00ms, 4.00ms)
Fig. 9 Mesh distributions near the shock at different moments (from left to right: t=2.00ms, 3.00ms, 4.00ms)
![]()
图 11 加速过程弹丸和弹托的受力曲线
Fig. 11 Aerodynamic force curves of projectile and sabots in the accelerated process
![]()
图 14 模型出膛过程的“虚拟挡板”示意图
Fig. 14 Schematic of virtual baffles in the process of themodel leaving the muzzle
![]()
图 15 分离阶段不同时刻马赫数云图
Fig. 15 Mach iso-contours at different moments in the process of sabot separation
-
[1] 任国民.弹道靶技术及其发展[J].弹道学报, 1994(1):90-96. http://d.old.wanfangdata.com.cn/Conference/49185 Ren G M. Technology of ballistics range and its development[J]. Journal of Ballistics, 1994(1):90-96. http://d.old.wanfangdata.com.cn/Conference/49185
[2] 唐恩凌, 李志秋.二级轻气炮中组合式弹托分离器的应用[J].沈阳理工大学学报, 2012, 31(1):84-87. DOI: 10.3969/j.issn.1003-1251.2012.01.022 Tang E L, Li Z Q. The application of combined type dissociator of projectile from its seat in two-stage light gas gun[J]. Journal of Shenyang Ligong University, 2012, 31(1):84-87. DOI: 10.3969/j.issn.1003-1251.2012.01.022
[3] Gouge M J, Combs S K, Fisher P W, et al. Design considerations for single-stage and two-stage pneumatic pellet injectors[J]. Review of Scientific Instruments, 1989, 60(4):575-575. https://www.researchgate.net/publication/224501005_Design_considerations_for_single-stage_and_two-stage_pneumatic_pellet_injectors
[4] 庄宇, 陆欣.二级轻气炮内弹道过程数学建模及数值仿真[J].兵器装备工程学报, 2016, 37(12):75-79. DOI: 10.11809/scbgxb2016.12.018 Zhuang Y, Lu X. Mathematical modeling and numerical simulation for interior ballistics process of two-stage light-gas gun[J]. Journal of Ordnance Equipment Engineering, 2016, 37(12):75-79. DOI: 10.11809/scbgxb2016.12.018
[5] 黄洁, 梁世昌, 李海燕, 等.二级轻气炮发射过程内弹道数值计算研究[J].空气动力学学报, 2013, 31(5):657-661. http://d.old.wanfangdata.com.cn/Periodical/kqdlxxb201305021 Huang J, Liang S C, Li H Y, et al. Numerical research on interior ballistics of the launch process of two-stage ligiht gas gun[J]. Acta Aerodynamica Sinica, 2013, 31(5):657-661. http://d.old.wanfangdata.com.cn/Periodical/kqdlxxb201305021
[6] 管小荣, 徐诚.二级轻气炮发射过程数学模型和计算方法[J].南京理工大学学报:自然科学版, 2007, 31(1):22-26. http://d.old.wanfangdata.com.cn/Periodical/njlgdxxb200701005 Guan X R, Xu C. Mathematical model and computing method for launch process of two-stage light-gas gun[J]. Journal of Nanjing University of Science and Technology, 2007, 31(1):22-26. http://d.old.wanfangdata.com.cn/Periodical/njlgdxxb200701005
[7] Zou D Y, Xu C G, Dong H B, et al. A shock-fitting technique for cell-centred finite volume methods on unstructured dynamic meshes[J]. Journal of Computational Physics, 2017, 345:866-882. DOI: 10.1016/j.jcp.2017.05.047
[8] 刘君, 邹东阳, 徐春光.基于非结构动网格的非定常激波装配方法[J].空气动力学学报, 2015, 33(1):10-16. DOI: 10.7638/kqdlxxb-2014.0109 Liu J, Zou D Y, Xu C G. An unsteady shock-fitting technique based on unstructured moving grids[J]. Acta Aerodynamica Sinica, 2015, 33(1):10-16. DOI: 10.7638/kqdlxxb-2014.0109
[9] Barth T J, Jespersen D C. The design and application of upwind schemes on unstructured meshes[C]//Proc of the 27th Aerospace Science Meeting. 1989.
[10] 阎超.计算流体力学方法与应用[M].北京:北京航空航天大学出版社, 2012. [11] 许和勇, 叶正寅.悬停共轴双旋翼干扰流动数值模拟[J].航空动力学报, 2011, 26(2):453-457. http://d.old.wanfangdata.com.cn/Periodical/hkdlxb201102032 Xu H Y, Ye Z Y. Numerical simulation of interaction unsteady flows around co-axial rotors in hover[J]. Journal of Aerospace Power, 2011, 26(2):453-457. http://d.old.wanfangdata.com.cn/Periodical/hkdlxb201102032
[12] 郭正, 刘君, 瞿章华.非结构动网格在三维可动边界问题中的应用[J].力学学报, 2003, 35(2):140-146. http://d.old.wanfangdata.com.cn/Periodical/lxxb200302003 Guo Z, Liu J, Qu Z H. Dynamic unstructured grid method with applications to 3D unsteady flows involving moving boundaries[J]. Acta Mechanica Sinica, 2003, 35(2):140-146. http://d.old.wanfangdata.com.cn/Periodical/lxxb200302003
[13] 伍贻兆, 田书玲, 夏健.基于非结构动网格的非定常流数值模拟方法[J].航空学报, 2011, 32(1):15-26. http://d.old.wanfangdata.com.cn/Periodical/hkxb201101002 Wu Y Z, Tian S L, Xia J. Unstructured grid methods for unsteady flow simulation[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(1):15-26. http://d.old.wanfangdata.com.cn/Periodical/hkxb201101002
[14] 桑为民, 李凤蔚, 鄂秦.应用笛卡尔非结构切割网格进行外挂物投放的数值模拟[J].计算物理, 2002, 19(3):268-272. DOI: 10.3969/j.issn.1001-246X.2002.03.017 Sang W M, Li F W, E Q. Numerical simulation of the store separation using unstructured cartesian cutted grid[J]. Chinese Journal of Computational Physics, 2002, 19(3):268-272. DOI: 10.3969/j.issn.1001-246X.2002.03.017
[15] Murman S M, Aftosmis M J, Berger M J. Implicit approaches for moving boundaries in a 3-D Cartesian method[C]//Proc of the 41st Aerospace Sciences Meeting and Exhibit. 2003.
[16] Batina J T. Unsteady Euler airfoil solutions using unstructured dynamic meshes[J]. AIAA Journal, 1989, 28(8):1381-1388. DOI: 10.2514-3.25229/
[17] Jay C, Carpenter M H. Computational considerations for the simulation of shock-induced sound[R]. NASA-TM-110222, 1995.
[18] Onofri M, Paciorri R. Shock fitting:classical techniques, recent developments, and memoirs of Gino Moretti[M]. Springer, 2017.
[19] 邹东阳, 刘君, 邹丽.可压缩流动激波装配方法在格心型有限体积中的应用[J].航空学报, 2017, 38(11):121363. http://www.cnki.com.cn/Article/CJFDTotal-HKXB201711013.htm Zou D Y, Liu J, Zou L. Applications of shock-fitting technique for compressible flow in cell-centered finite volume methods[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(11):121363. http://www.cnki.com.cn/Article/CJFDTotal-HKXB201711013.htm
[20] 王巍.有相对运动的多体分离过程非定常数值算法研究及实验验证[D].长沙: 国防科学技术大学, 2008. Wang W. Numerical simulation technique research and experiment verification for unsteady multi-body flowfield involving relative movement[D]. Chang Sha: National University of Defense Technology, 2008.
-
期刊类型引用(2)
1. 常思源，白晓征，崔小强，刘君. 一种改进的非定常激波装配算法. 航空学报. 2020(02): 163-176 . 
百度学术
2. 刘君，韩芳. 有关有限差分高精度格式两个应用问题的讨论. 空气动力学学报. 2020(02): 244-253 . 百度学术
其他类型引用(0)
下载:
计量
- 文章访问数: 239
- HTML全文浏览量: 134
- PDF下载量: 17
- 被引次数: 2
