Experimental study on the effect of angle of attack on airfoil boundary layer
-
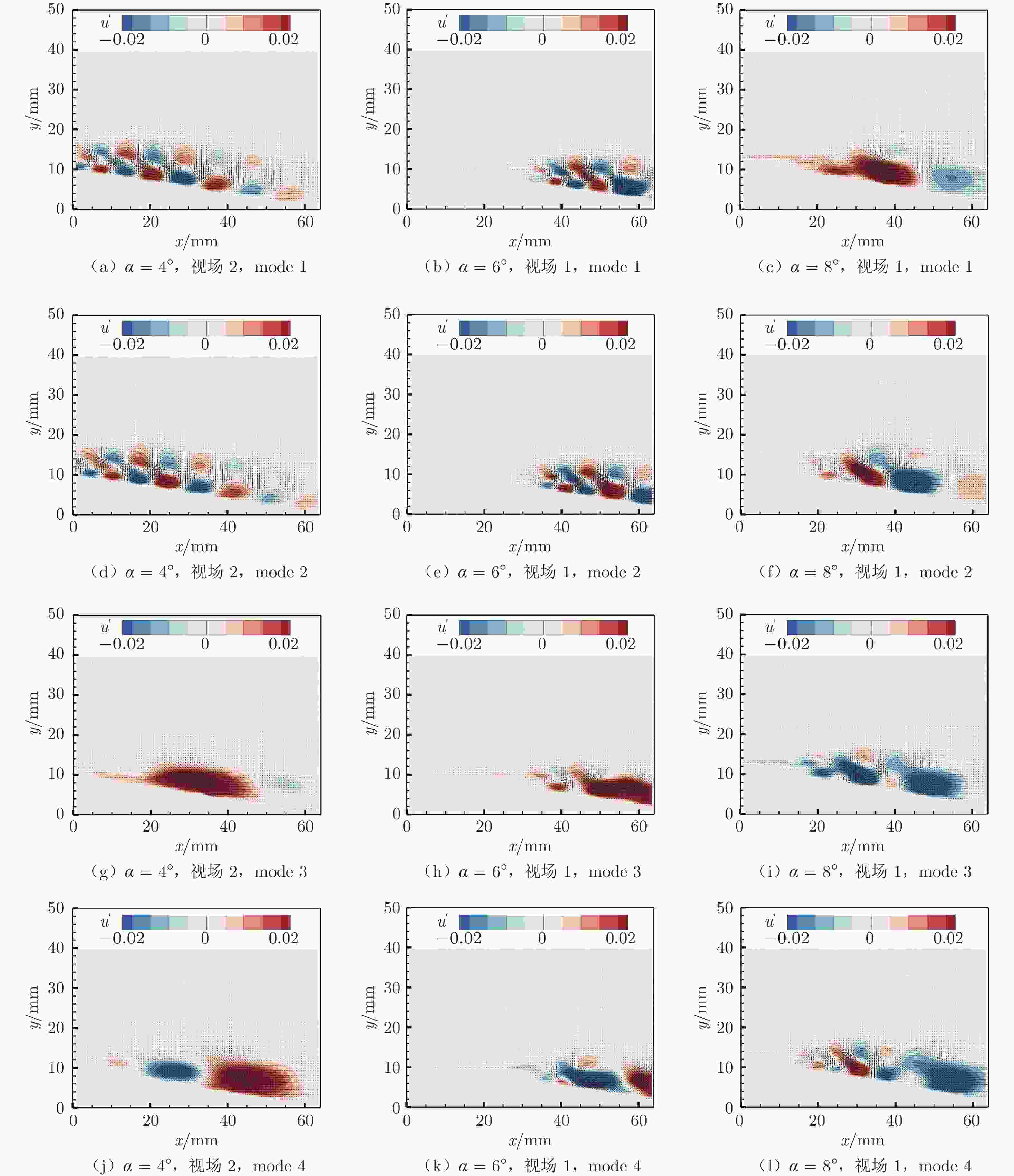
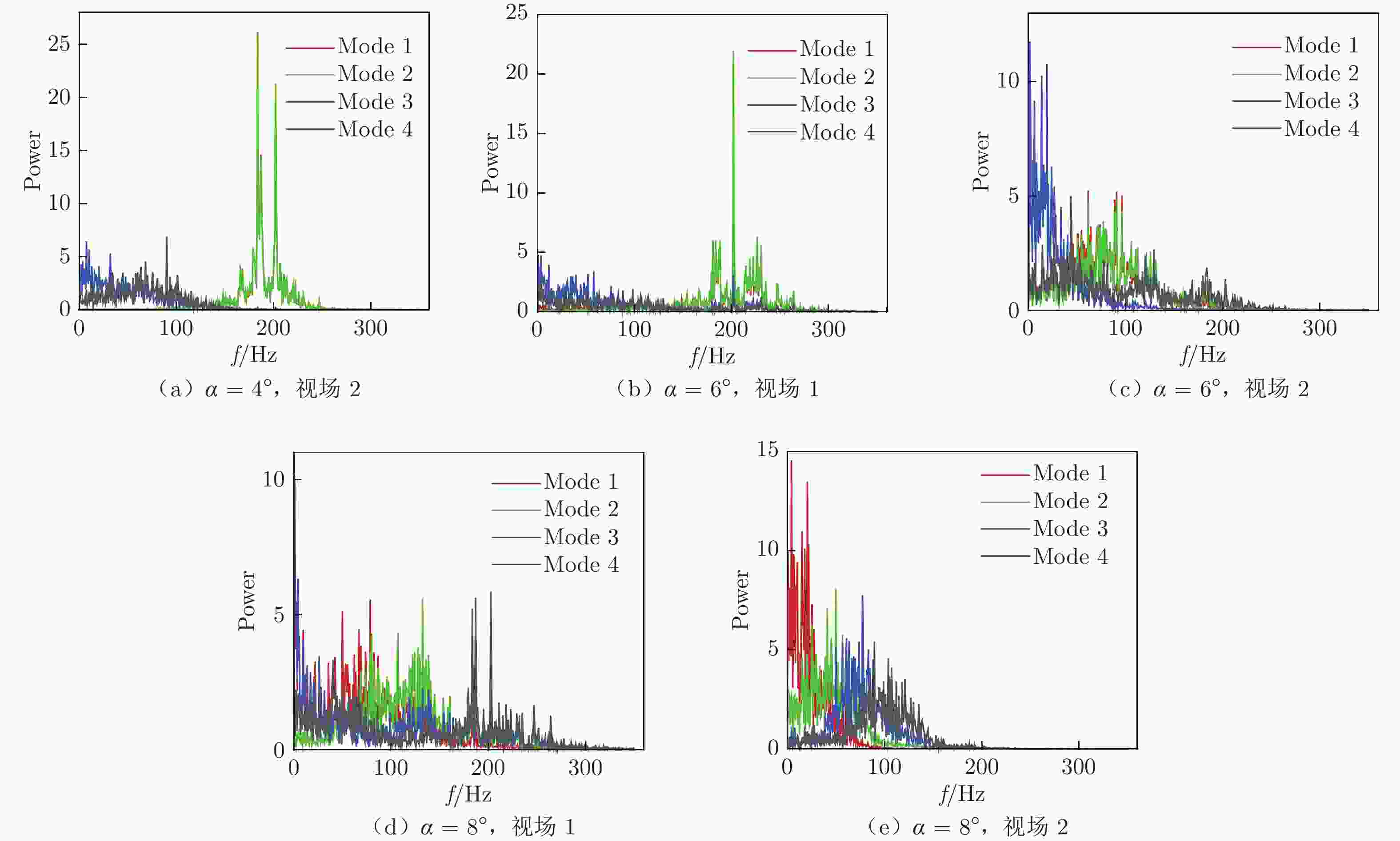
摘要: 为深入了解迎角对翼型边界层的影响,开展了SD7003翼型的TR–PIV实验研究。对比了迎角为4°、6°、8°工况下翼型吸力面的平均速度、雷诺切应力等统计量的分布,并对实验数据进行了本征正交分解(POD)模态分析,详细分析了不同工况下各阶模态中的流动结构及其频谱特征。研究发现,随着迎角增大,分离泡位置向翼型前缘移动,分离泡厚度增大;分离泡内部和再附点附近存在较强的剪切运动;再附点附近有交替出现的正、反方向涡结构,而后涡结构随边界层发展不断变化;POD分解的各阶模态的能量大小与其所包含结构的尺度和模态频率有关;随着迎角增大,流场中流动结构尺度增大,流场能量的频域分布由高频向低频移动。Abstract: In order to deeply understand the influence of the angle of attack on the airfoil boundary layer, a TR–PIV experimental study on the SD7003 airfoil is carried out. The distributions of statistics such as the average velocity of the airfoil suction surface and the Reynolds shear stress under the working conditions of the angle of attack α = 4°, 6° and 8° are compared. Proper orthogonal decomposition (POD) method is adopted for analysis of the experimental data. The flow structure in each mode and the frequency spectrum characteristics of the modes under different working conditions are analyzed in detail. The study finds that: with the increase of the angle of attack, the position of the separation bubble moves to the leading edge of the airfoil, and the thickness of the separation bubble increases; there is intensive shear motion inside the separation bubble and near the reattachment point; there are alternating positive and negative vortex structures near the reattachment point, and the vortex structures change continuously with the development of the boundary layer; the energy of each mode of POD decomposition is related to the scale of the structure contained and the mode frequency; with the increase of the angle of attack, the scale of the flow structures in the flow field increases, and the frequency domain distribution of flow field energy shifts from high frequency to low frequency.
-
Key words:
- airfoil /
- boundary layer /
- PIV /
- transition /
- flow structure /
- proper orthogonal decomposition
-
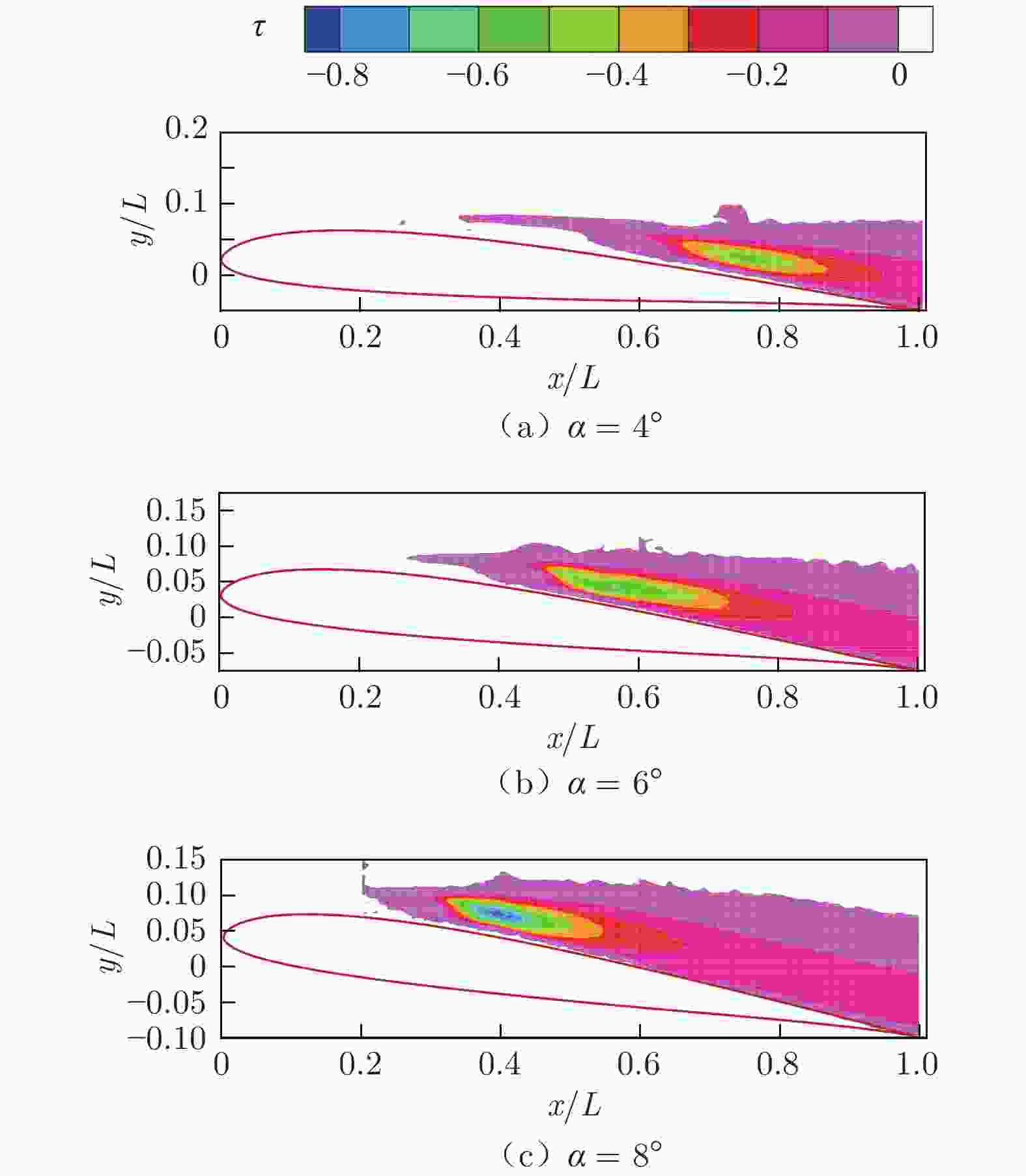
表 1 不同迎角下分离泡最大厚度、雷诺切应力最大值、最大雷诺切应力位置及再附点位置对比
Table 1. Comparison of the maximum thickness of bubbles, the maximum and locations of Reynolds shear stress, and reattachment points against angles of attack
α δmax/mm τmax/(N·m−2) xτ,max xr 4° 2.9579 −0.5595 0.7616L 0.7257L 6° 3.1087 −0.6214 0.5662L 0.5224L 8° 3.7173 −0.8461 0.3977L 0.4017L -
[1] 李锋, 白鹏, 石文, 等. 微型飞行器低雷诺数空气动力学[J]. 力学进展, 2007, 37(2): 257–268. doi: 10.3321/j.issn:1000-0992.2007.02.009LI F, BAI P, SHI W, et al. Low Reynolds number aerodynamics of micro air vehicles[J]. Advances in Mecha-nics, 2007, 37(2): 257–268. doi: 10.3321/j.issn:1000-0992.2007.02.009 [2] LIN J C M, PAULEY L L. Low-Reynolds-number separation on an airfoil[J]. AIAA Journal, 1996, 34(8): 1570–1577. doi: 10.2514/3.13273 [3] LISSAMAN P S. Low-Reynolds-number airfoils[J]. Annual Review of Fluid Mechanics, 1983, 15(1): 223–239. doi: 10.1146/annurev.fl.15.010183.001255 [4] HORTON H P. Laminar separation bubbles in two and three dimensional incompressible flow[D]. London: Queen Mary University of London, 1968 [5] ALAM M, SANDHAM N D. Direct numerical simulation of ‘short’ laminar separation bubbles with turbulent reattach-ment[J]. Journal of Fluid Mechanics, 2000, 410: 1–28. doi: 10.1017/s0022112099008976 [6] SELIG M, GUGLIELMO J, BROERN A, et al. Experiments on airfoils at low Reynolds numbers[C]//Proc of the 34th Aerospace Sciences Meeting and Exhibit. 1996. doi: 10.2514/6.1996-62 [7] BREHM C, MACK S, GROSS A, et al. Investigations of an airfoil at low Reynolds number conditions[C]//Proc of the 4th Flow Control Conference. 2008. doi: 10.2514/6.2008-3765 [8] GROSS A, FASEL H. Numerical investigation of separation for airfoils at low Reynolds numbers[C]//Proc of the 40th Fluid Dynamics Conference and Exhibit. 2010. doi: 10.2514/6.2010-4736 [9] 白鹏, 李锋, 詹慧玲, 等. 翼型低Re数小攻角非线性非定常层流分离现象研究[J]. 中国科学 (物理学 力学 天文学), 2015, 45(2): 41–52. doi: 10.1360/sspma2014-00212BAI P, LI F, ZHAN H L, et al. Study about the non-linear and unsteady laminar separation phenomena around the airfoil at low Reynolds number with low incidence[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2015, 45(2): 41–52. doi: 10.1360/sspma2014-00212 [10] ZHOU Y, WANG Z J. Implicit large eddy simulation of low Reynolds number transitional flow over a wing using high-order spectral difference method[C]//Proc of the 40th Fluid Dynamics Conference and Exhibit. 2010. doi: 10.2514/6.2010-4442 [11] BURGMANN S, BRÜCKER C, SCHRÖDER W. Scanning PIV measurements of a laminar separation bubble[J]. Experiments in Fluids, 2006, 41(2): 319–326. doi: 10.1007/s00348-006-0153-6 [12] BURGMANN S, DANNEMANN J, SCHRÖDER W. Time-resolved and volumetric PIV measurements of a transitional separation bubble on an SD7003 airfoil[J]. Experiments in Fluids, 2008, 44(4): 609–622. doi: 10.1007/s00348-007-0421-0 [13] OL M, MCCAULIFFE B, HANFF E, et al. Comparison of laminar separation bubble measurements on a low Reynolds number airfoil in three facilities[C]//Proc of the 35th AIAA Fluid Dynamics Conference and Exhibit. 2005. doi: 10.2514/6.2005-5149 [14] 朱志斌, 刘强, 白鹏. 低雷诺数翼型层流分离现象大涡模拟方法[J]. 空气动力学学报, 2019, 37(6): 915–923. doi: 10.7638/kqdlxxb-2018.0025ZHU Z B, LIU Q, BAI P. Large eddy simulation method for the laminar separation phenomenon on low Reynolds number airfoils[J]. Acta Aerodynamica Sinica, 2019, 37(6): 915–923. doi: 10.7638/kqdlxxb-2018.0025 [15] 朱志斌, 尚庆, 白鹏, 等. 翼型低雷诺数层流分离现象随雷诺数的演化特征[J]. 航空学报, 2019, 40(5): 122528. doi: 10.7527/S1000-6893.2018.22528ZHU Z B, SHANG Q, BAI P, et al. Evolution of laminar separation phenomenon on low Reynolds number airfoil at different Reynolds numbers[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(5): 122528. doi: 10.7527/S1000-6893.2018.22528 [16] ZHOU Y, WANG Z J. Effects of surface roughness on separated and transitional flows over a wing[J]. AIAA Journal, 2012, 50(3): 593–609. doi: 10.2514/1.j051237 [17] KAMARI D, TADJFAR M, MADADI A. Optimization of SD7003 airfoil performance using TBL and CBL at low Reynolds numbers[J]. Aerospace Science and Technology, 2018, 79: 199–211. doi: 10.1016/j.ast.2018.05.049 [18] 朱玉杰, 孙振生, 张炜, 等. 低Reynolds数翼型绕流主动控制技术[J]. 气体物理, 2017, 2(6): 18–27. doi: 10.19527/j.cnki.2096-1642.2017.06.003ZHU Y J, SUN Z S, ZHANG W, et al. Active control of low Reynolds number airfoil flow by implicit large eddy simulation[J]. Physics of Gases, 2017, 2(6): 18–27. doi: 10.19527/j.cnki.2096-1642.2017.06.003 [19] LUMLEY J L. The structure of inhomogeneous turbu-lence[J]. Atmospheric Turbulence and Radio Wave Propa-gation, 1967: 166–178. doi: 10.1007/BF00271656 [20] BERKOOZ G, HOLMES P, LUMLEY J L. The proper orthogonal decomposition in the analysis of turbulent flows[J]. Annual Review of Fluid Mechanics, 1993, 25(1): 539–575. doi: 10.1146/annurev.fl.25.010193.002543 [21] SIROVICH L. Turbulence and the dynamics of coherent structures. I. Coherent structures[J]. Quarterly of Applied Mathematics, 1987, 45(3): 561–571. doi: 10.1090/qam/910462 -







 下载:
下载: