The kinematics and performance of zebrafish C-shaped maneuvering
-
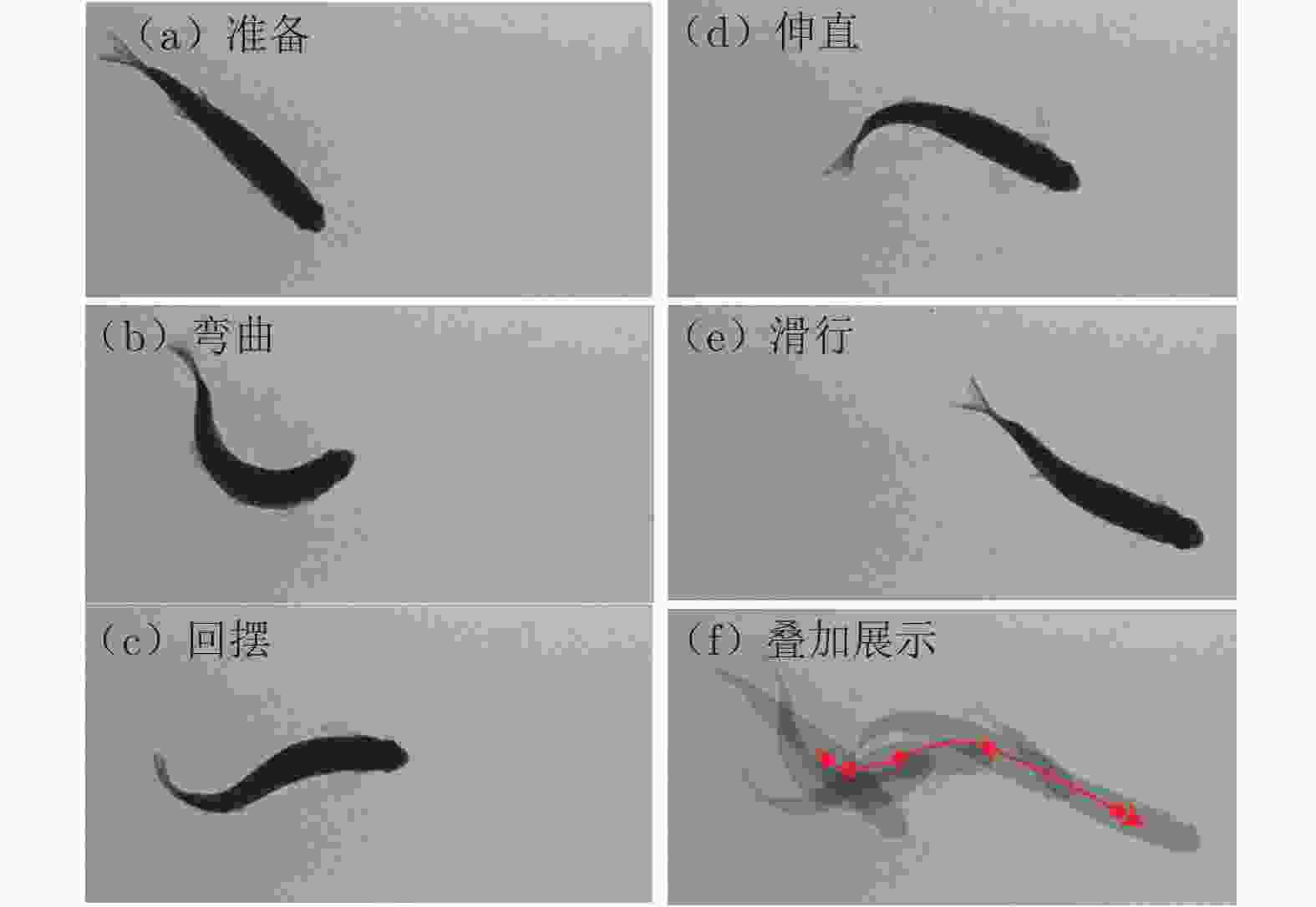
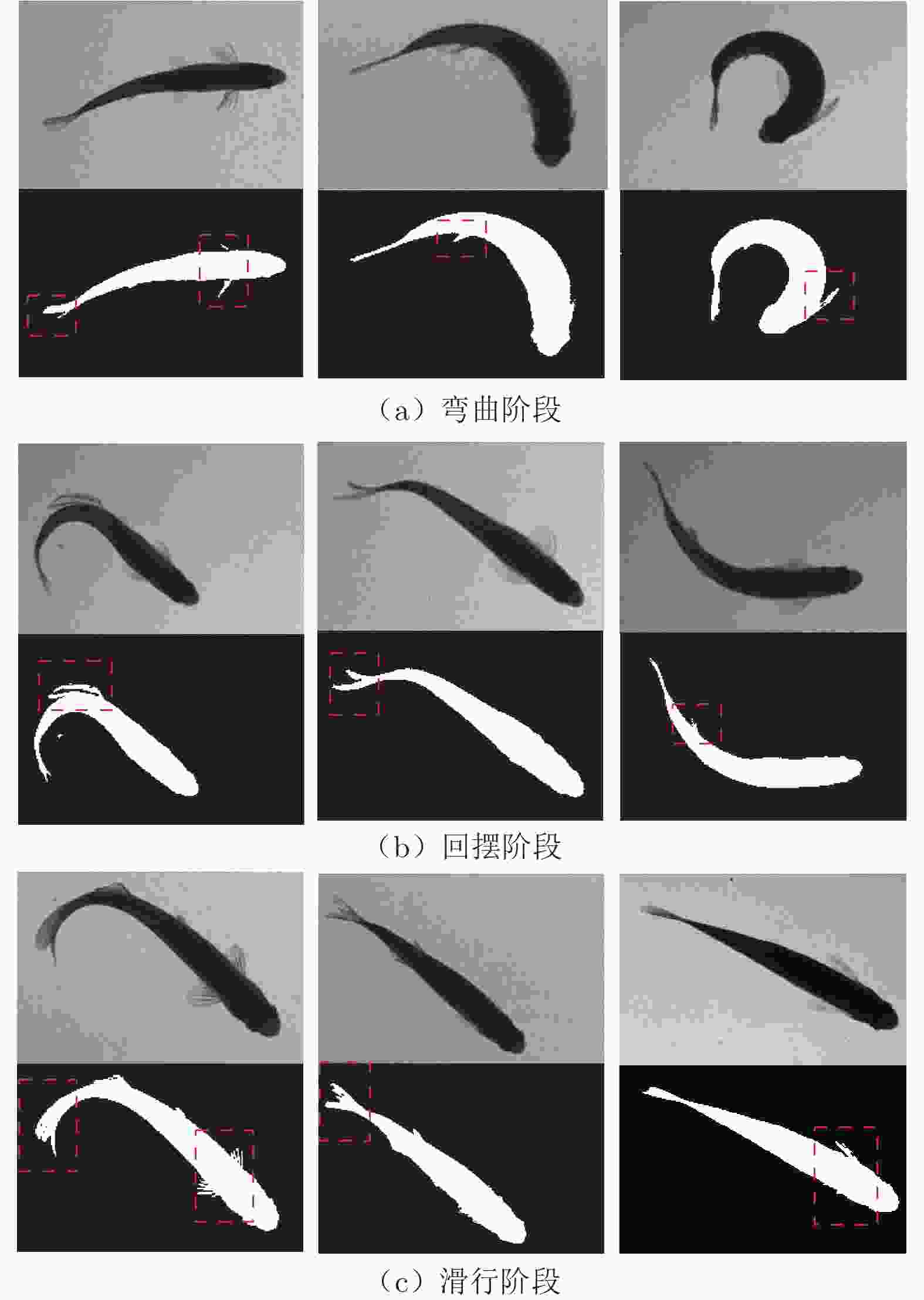
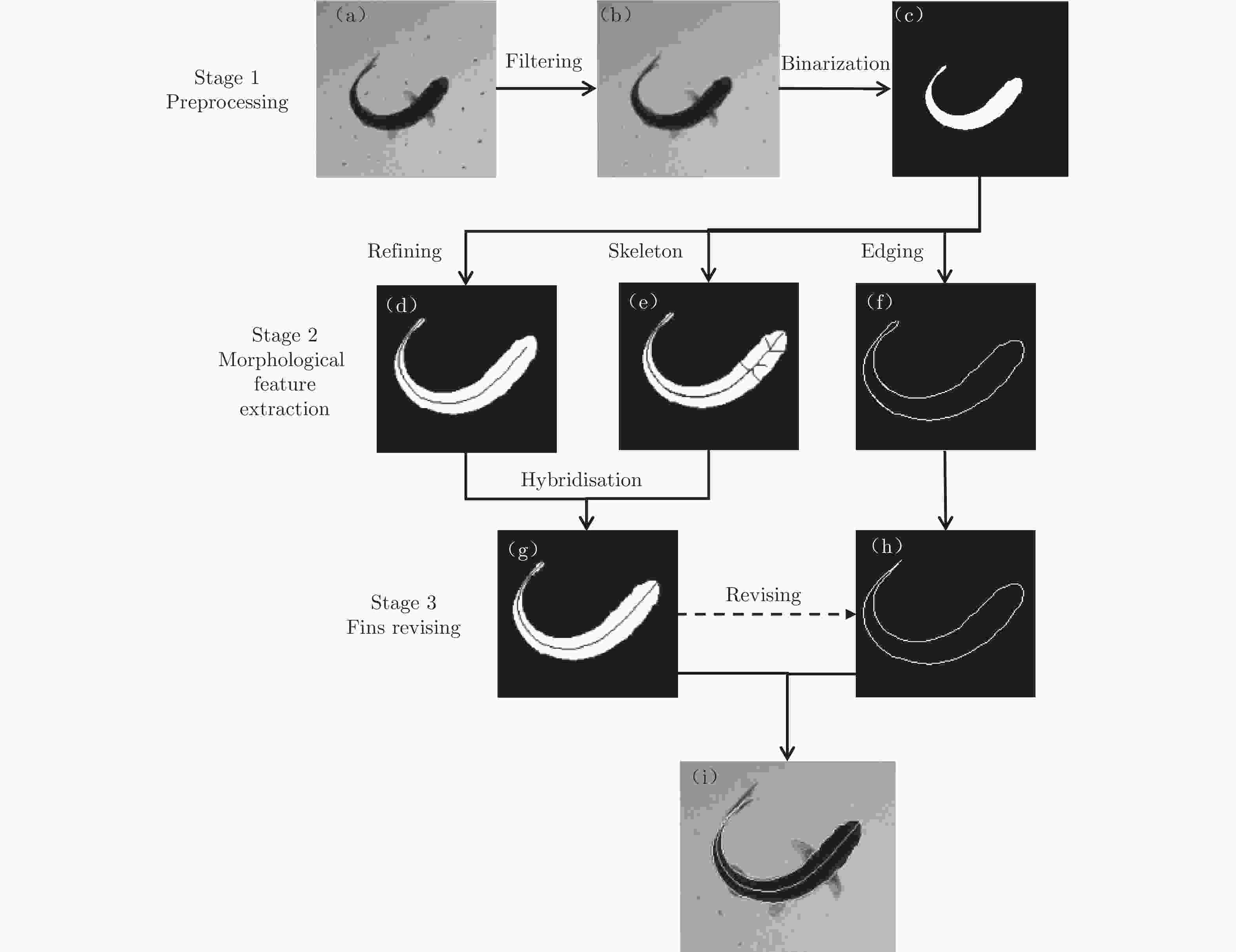
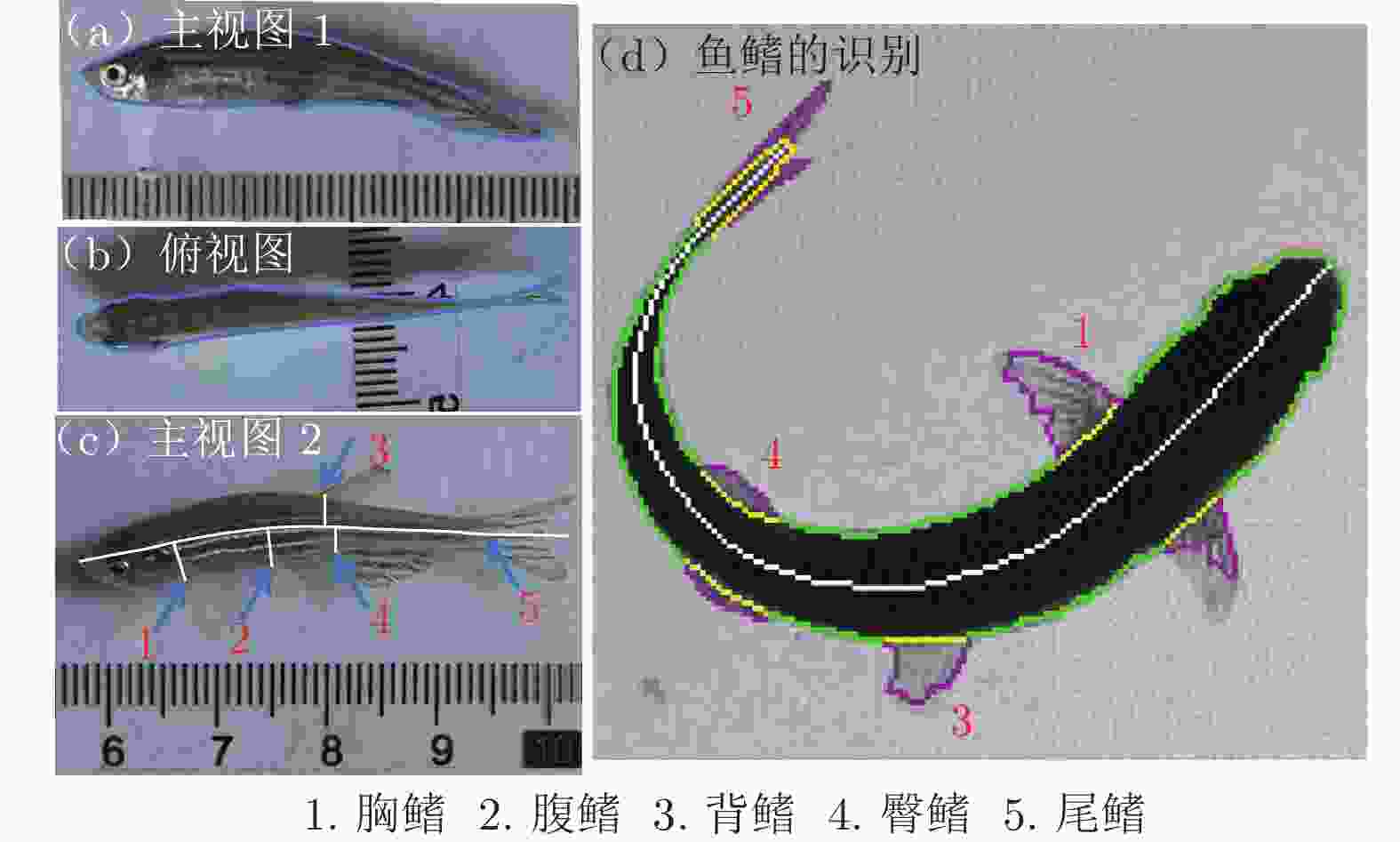
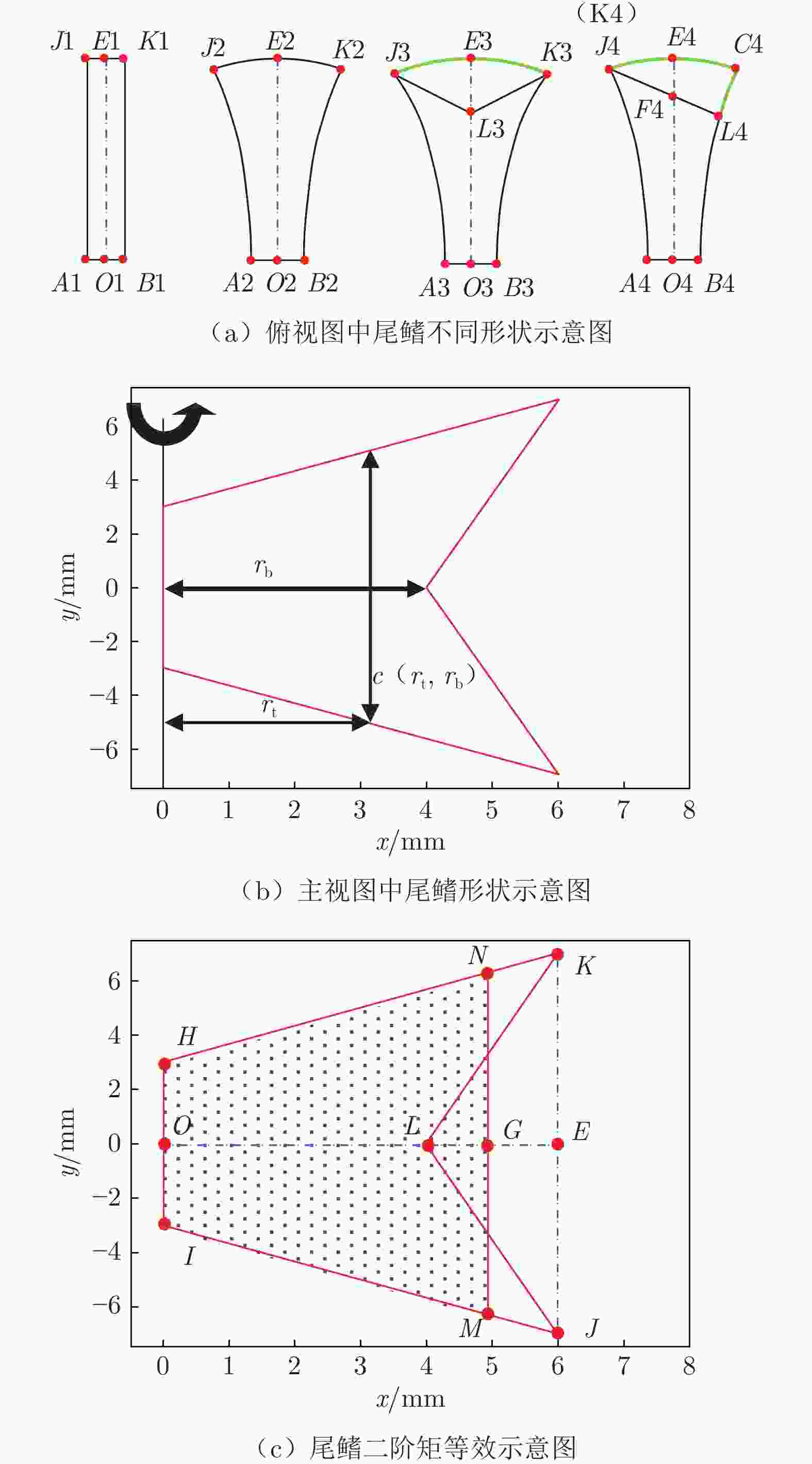
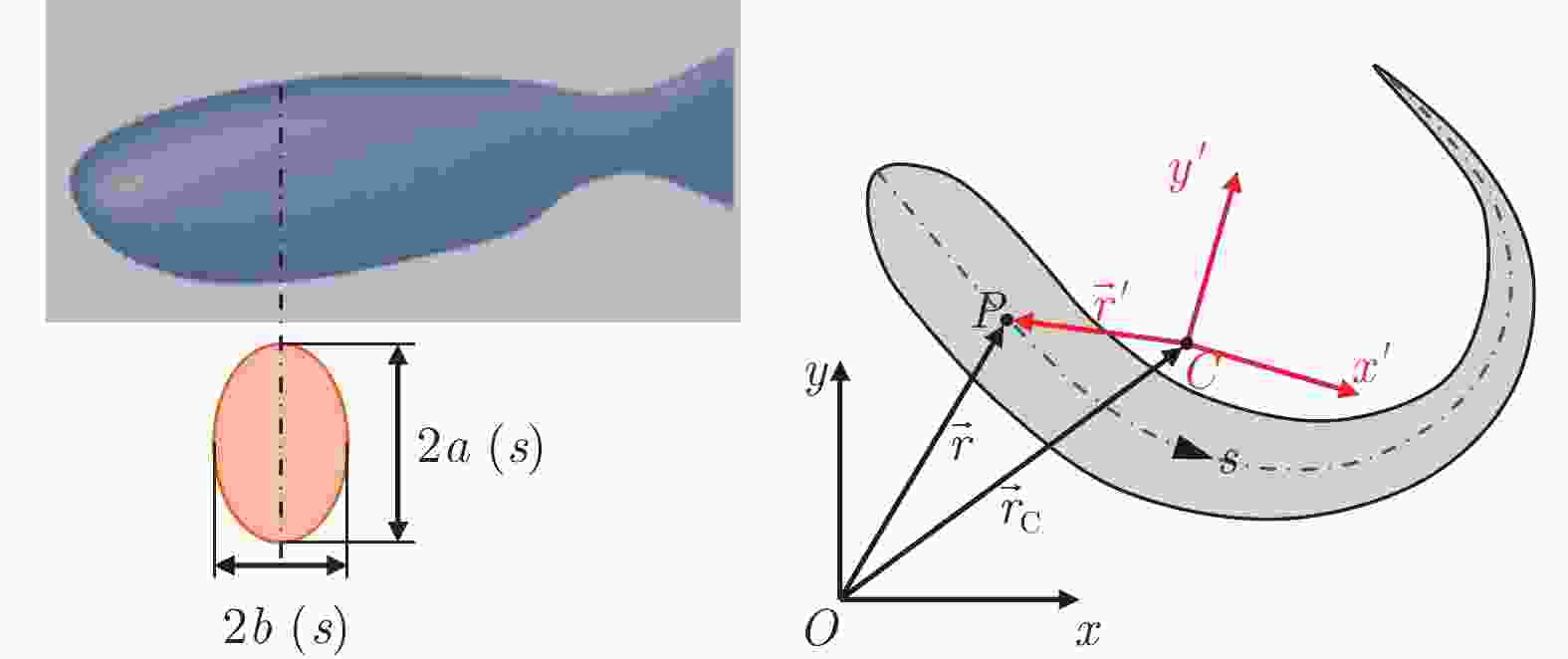
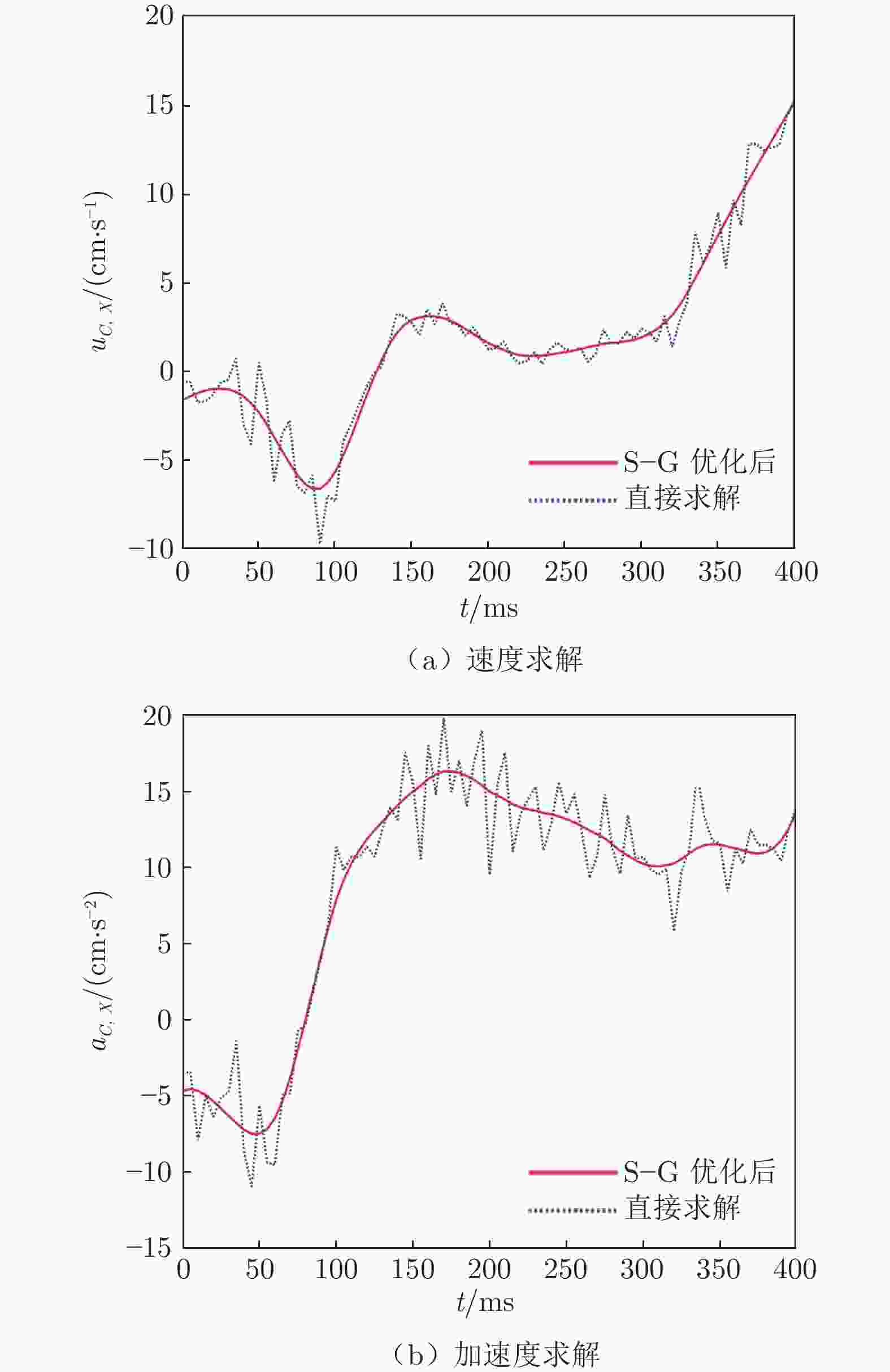
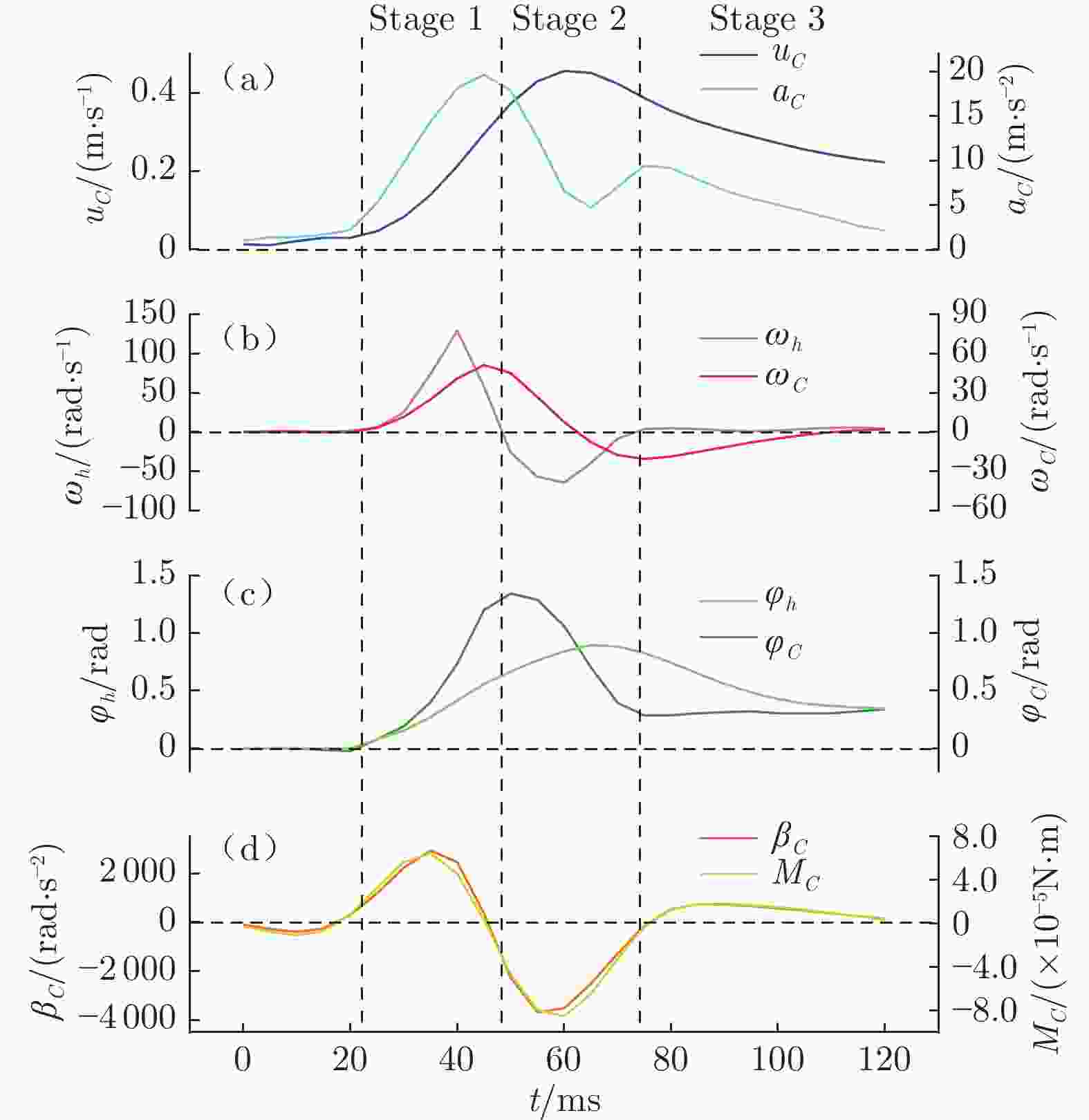
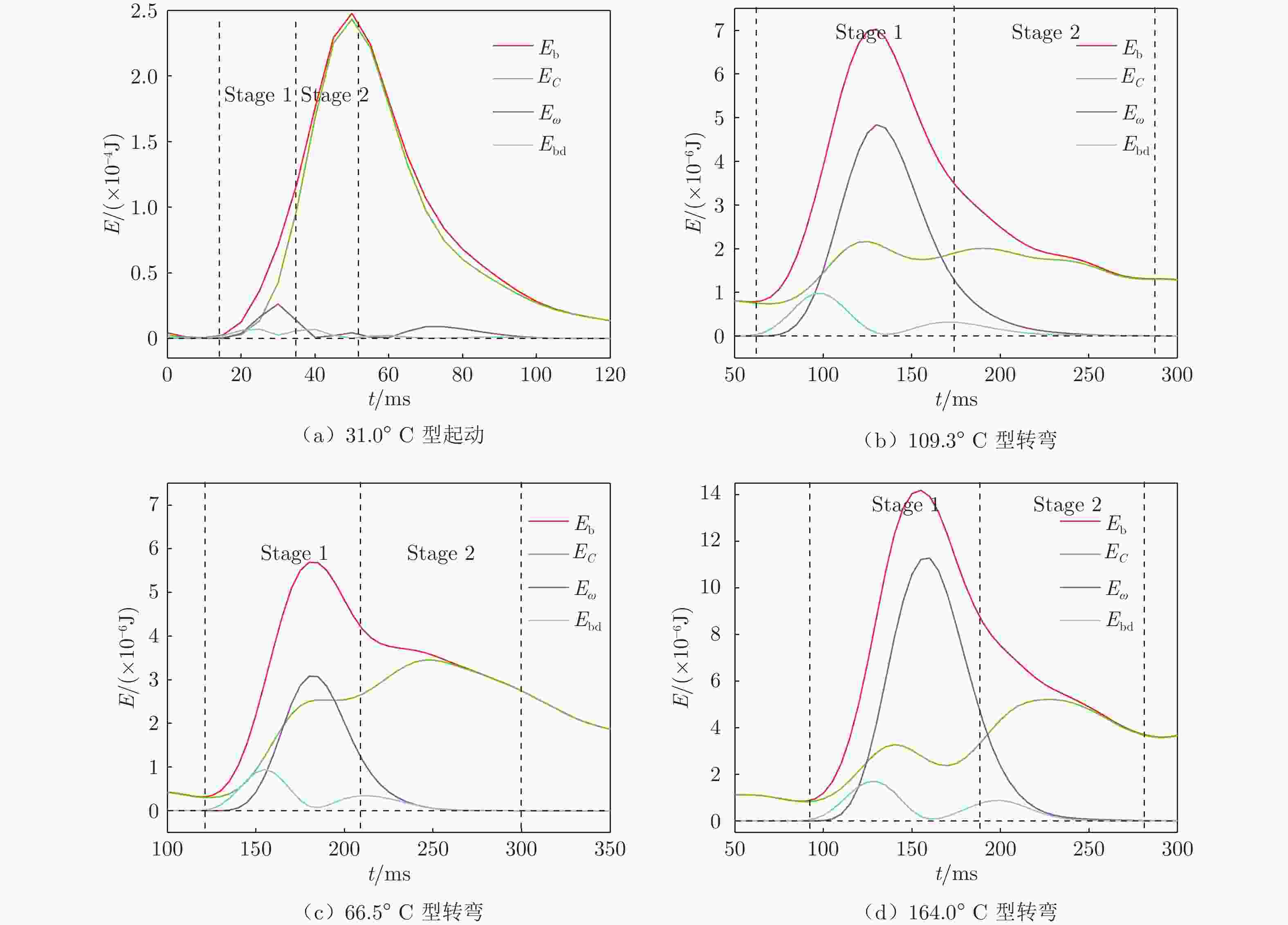
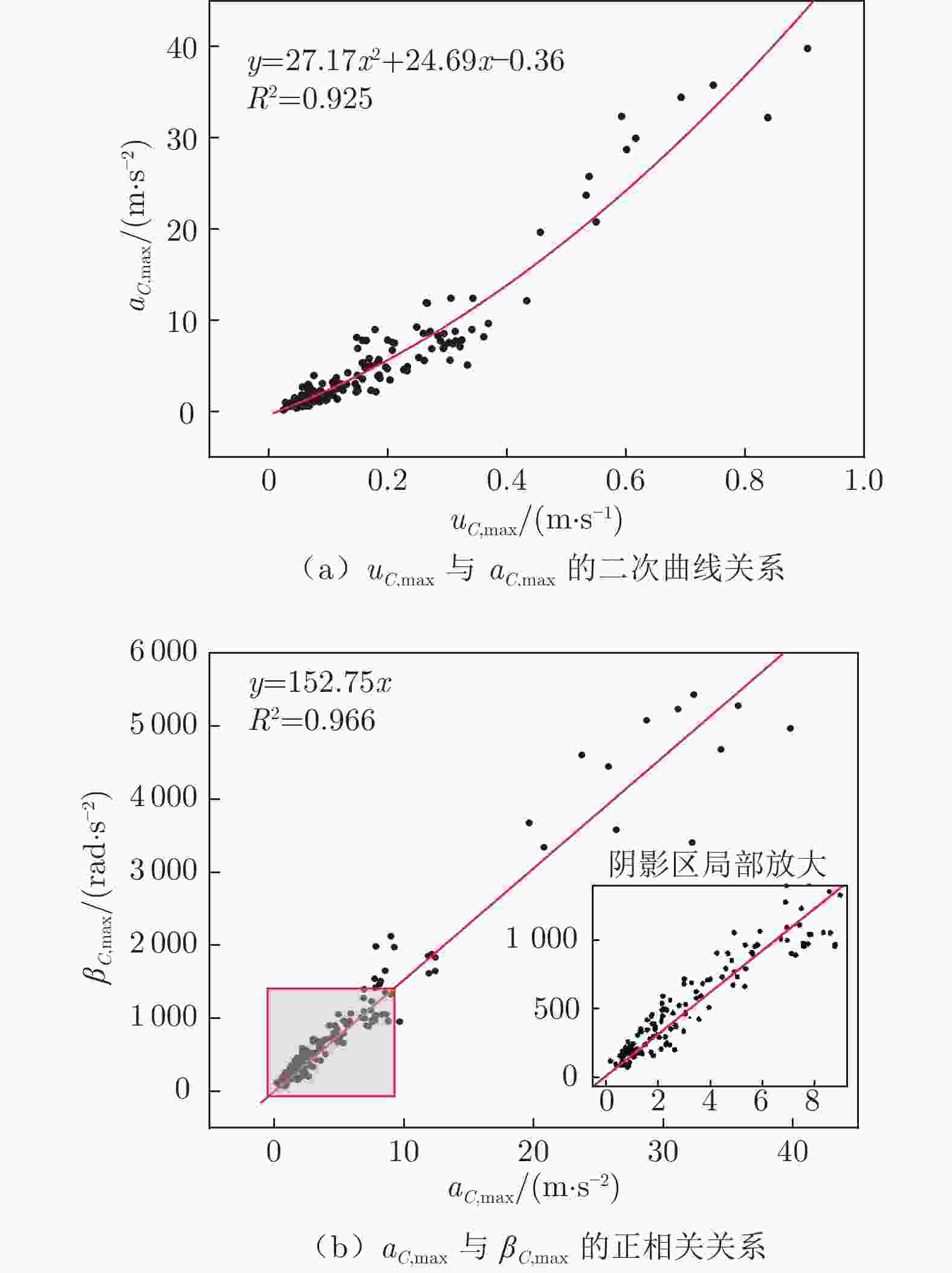
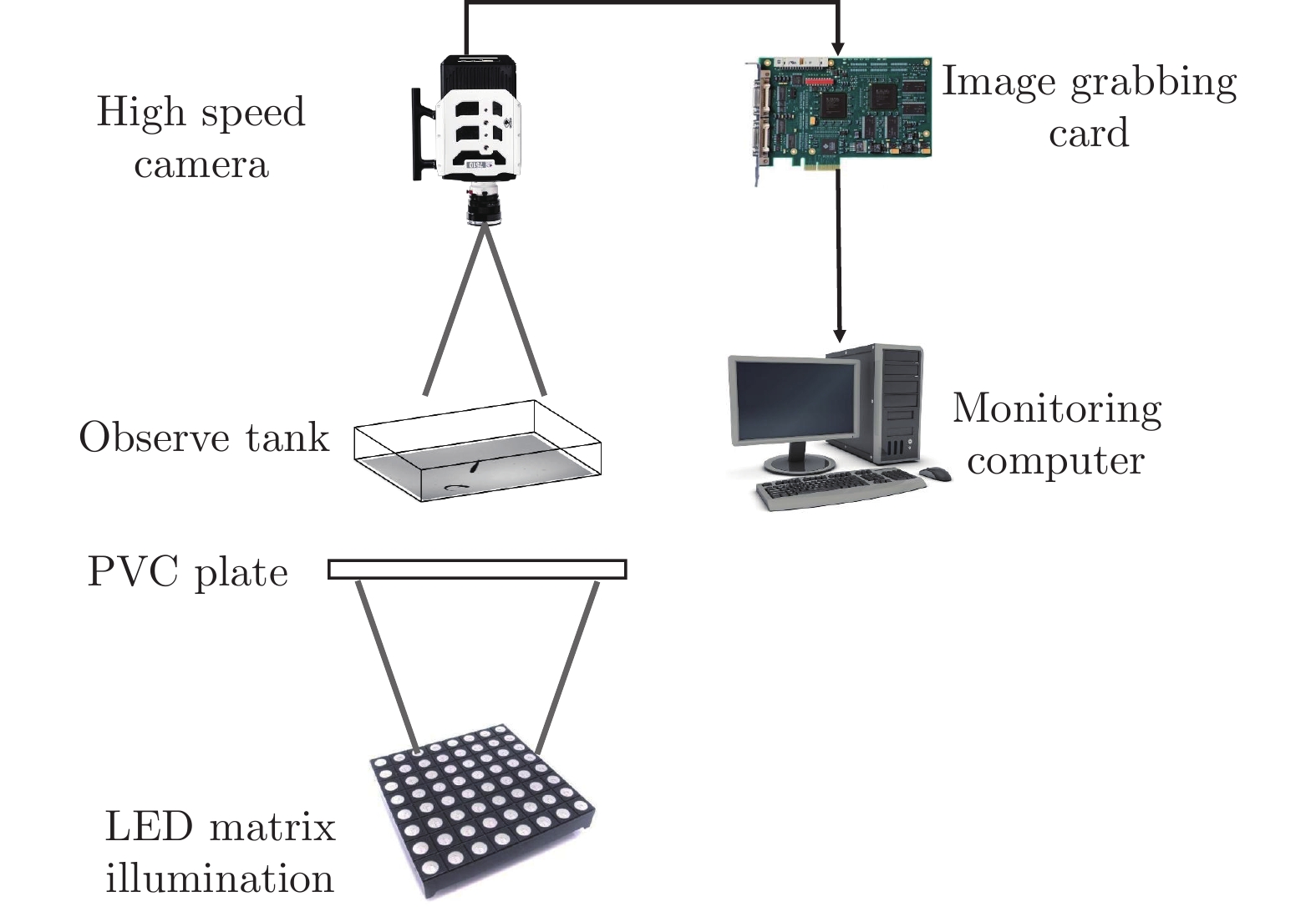
摘要: 在鱼类机动性能研究中，获取高精度运动学和动力学实验数据至关重要。本文搭建基于机器视觉的高速摄影平台，获取了斑马鱼C型机动运动的顶视序列图像；使用数学形态学算法提取图像中的鱼体外轮廓和中线，建立了简化的三维鱼体模型；通过“鱼–水”系统的动量和动量矩守恒算法，获得鱼体的运动学数据，并分析了作用于鱼体的流体动力和机械能的变化规律。在鱼体模型建立过程中，对尾鳍进行面积的二阶矩等效处理，完成了尾鳍长度的合理修正。经一系列标准算例验证，采用数字图像处理技术重构的动力学数据与标准模型误差在3.1%以内。结果表明：鱼体C型机动运动中最大加速度与最大角加速度存在线性关系；C型起动中平动能占主导，C型转弯中转动能占主导。Abstract: It is difficult to obtain the complete kinematics and hydrodynamics from the experiments in the study of fish C-type fast-start, which can be divided into C-start and C-turn by the duration of maneuvers. Using high-speed photography, a series of top-view images of zebrafish's C-shaped maneuvering were obtained on the self-built platform based on machine vision. A simplified three-dimensional (3D) fish model was established according to the outline and midline of the fish body extracted from the images by using a mathematical morphology algorithm. Then, due to the conservation of the linear and angular momentum, the complete kinematic and hydrodynamic data during the whole maneuver motion can be obtained and the translational and rotational energy can be distinguished from the total kinetic energy of the zebrafish body. The modification of the caudal fin length is a highlight in 3D modeling, which is based on the equivalence of the area second-moment of a flapping 3D plate. Through the benchmark validation, the maximum geometric error of the digital image processing is less than 3.1%. The results show that the maximum acceleration in all the C-type fast-start is linearly related to the maximum angular acceleration, and the rotational energy of C-turn is dominant in the kinetic energy while the translational energy of C-start is dominant.
-
Key words:
- zebrafish /
- C-shaped maneuvering /
- digital image processing /
- kinematics /
- hydrodynamics /
- energetics.
-
图 1 斑马鱼动作捕获实验平台示意图
Figure 1. Sketch map of experimental platform for zebrafish swimming
图 3 鱼体机动运动中弯曲、回摆和滑行阶段代表性动作与其二值化效果
Figure 3. Typical images and their binarization identification of the fish body and fins during bending, swinging back and coasting motions
图 7 鱼体的三维重构示意图（左）及惯性系与质心系间关系（右）
Figure 7. Sketch map of fish 3D reconstruction model Relationship between inertial system and centroid system in maneuvering motion
图 8 S−G滤波对运动学数据捕获的优化效果
Figure 8. Effect of S−G filtering on kinematics data acquisition
图 9 一次C型起动中鱼体各运动学数据随时间的变化
Figure 9. Kinematics vary over time in a fish C-start motion
图 10 鱼体 C 型机动运动中机械能及其分量随时间的变化
Figure 10. Variation of mechanical energy and its components with time in zebrafish C-shaped maneuvering
图 11 斑马鱼C型机动运动统计规律分析
Figure 11. Statistical analysis of zebrafish C-shaped maneuvering
表 1 标准算例参数设置与运动学数据相对误差
Table 1. Parameter setting of standard example and kinematic data error
运动模式 分辨率/(像素×像素) 运动模型参数 $E_{{\rm{R}},X} $ $E_{ {\rm{R} },{u_C} }$ $E_{{\rm{R}},a_C} $ $E_{ {\rm{R} },{w_C} }$ $E_{ {\rm{R} },{\beta_C} }$ 匀速直线 1080×800 $\bar u_C(t)=1\;{\rm{m} }/{\rm{s} }$ 0.18% 0.20% — — — 匀速直线 2160×1600 $\bar u_C(t)=1\;{\rm{m} }/{\rm{s} }$ 0.09% 0.10% — — — 匀加速直线 1080×800 $u_C(t)=10 t\;{\rm{m} }/{\rm{s} }$ 0.19% 0.26% 1.10% — — 匀速圆周 1080×800 $\omega_C(t)=4\pi\; {\rm{rad} }/{\rm{s} }$ 0.41% 1.80% 2.96% 1.20% — 匀速圆周 2160×1600 $\omega_C(t)=4\pi\; {\rm{rad} }/{\rm{s} }$ 0.21% 0.80% 1.54% 0.70% — 匀加速圆周 1080×800 $\omega_C(t)=40\pi t\; {\rm{rad} }/{\rm{s} }$ 0.40% 1.60% 2.80% 1.14% 2.10% 波状摆动 1080×800 $y(s,t)=0.4\sin\left[2\pi\left(\dfrac{s}{4}-\dfrac{t}{0.5}\right)\right]\;{\rm{cm} }$ 0.15% 0.30% 1.27% 1.23% 3.07% 波状摆动 2160×1600 $y(s,t)=0.4\sin\left[2\pi\left(\dfrac{s}{4}-\dfrac{t}{0.5}\right)\right]\;{\rm{cm} }$ 0.08% 0.21% 0.83% 0.70% 2.10% 
下载: 导出CSV
-
[1] WEIHS D. The mechanism of rapid starting of slender fish1[J]. Biorheology, 2017, 10(3): 343–350. [2] DOMENICI P, BLAKE R W, et al. The kinematics and performance of fish fast-start swimming[J]. Journal of Experimental Biology, 1997, 200(8): 1165–1165. doi: 10.1242/jeb.200.8.1165 [3] DOMENICI P, BLAKE R W, et al. The kinematics and performance of the escape response in the angelfish (Pterophyllum eimekei)[J]. Journal of Experimental Biology, 1991, 156(1): 187–205. doi: 10.1242/jeb.156.1.187 [4] KASAPI M A, DOMENICI P, BLAKE R W, et al. The kinematics and performance of escape responses of the knifefish Xenomystus nigri[J]. Canadian Journal of Zoology, 1993, 71(1): 189–195. doi: 10.1139/z93-026 [5] LIU J, HU H. Mimicry of Sharp Turning Behaviors in a Robotic Fish[C]//Proceedings of the 2005 IEEE International Conference on Robotics and Automation. 2005. [6] GRAY J. Directional Control of Fish Movement[J]. Proceedings of the Royal Society of London, 1933, 113(781): 115–125. [7] WEIHS D. The mechanism of rapid starting of slender fish[J]. Biorheology, 1973, 10(3): 343–350. doi: 10.3233/BIR-1973-10308 [8] BASU S, DAVIDSON I, WAGSTAFF K. Constrained clustering: advances in algorithms, theory, and applications[M]. Florida: CRC Press, 2008. [9] BANG P I, YELICK P C, MALICKI J J, et al. High-throughput behavioral screening method for detecting auditory response defects in zebrafish[J]. Journal of Neuroscience Methods, 2002, 118(2): 177–187. doi: 10.1016/S0165-0270(02)00118-8 [10] TYTELL E D, LAUDER G V. The C-start escape response of Polypterus senegalus: bilateral muscle activity and variation during stage 1 and 2[J]. Journal of Experimental Biology, 2002, 205(Pt 17): 2591-2603. [11] MCHENRY M J. Mechanisms of helical swimming: asymmetries in the morphology, movement and mechanics of larvae of the ascidian Distaplia occidentalis[J]. Journal of Experimental Biology, 2001, 204(Pt 17): 2959. [12] WEI G, COSMAN P, BERRY, et al. Automatic tracking, feature extraction and classification of C elegans phenotypes[J]. Biomedical Engineering IEEE Transactions on, 2004, 51(10): 1811–1820. doi: 10.1109/TBME.2004.831532 [13] CRONIN C J, MENDEL J E, MUKHTAR S, et al. An automated system of measuring parameters of nematode sinusoidal movement[J]. BMC Genetics, 2005, 6(1): 5. doi: 10.1186/1471-2156-6-5 [14] FONTAINE E, LENTINK D, KRANENBARG S, et al. Automated visual tracking for studying the ontogeny of zebrafish swimming[J]. Journal of Experimental Biology, 2008, 211(8): 1305. doi: 10.1242/jeb.010272 [15] GUO Y, XIONG Z, VERBEEK F J. An efficient and robust hybrid method for segmentation of zebrafish objects from bright-field microscope images[J]. Machine Vision and Applications, 2018, 29(8): 1211–1225. doi: 10.1007/s00138-018-0934-y [16] LIU G, GENG B, ZHENG X, et al. An image-guided computational approach to inversely determine in vivo material properties and model flow-structure interactions of fish fins[J]. Journal of Computational Physics, 2019, 392: 578–593. doi: 10.1016/j.jcp.2019.04.062 [17] 张冰冰, 余永亮. 斑马鱼C型起动中动力学特性的活体实验研究[J]. 实验力学, 2014, 29(6): 10. [18] 施特格. 机器视觉算法与应用[M]. 北京: 清华大学出版社, 2008. [19] GONZALEZ R C, WOODS R E. Digital image processing[J]. Prentice Hall International, 2008, 28(4): 484–486. [20] 郭春钊, 汪增福. 基于序列图像的鱼游运动机理分析[J]. 实验力学, 2005, 20(04): 525–531. doi: 10.3969/j.issn.1001-4888.2005.04.006 [21] BORAZJANI I, SOTIROPOULOS F. Numerical investigation of the hydrodynamics of carangiform swimming in the transitional and inertial flow regimes[J]. Journal of Experimental Biology, 2008, 211(Pt 10): 1541–1558. [22] DONG H, BOZKURTTAS M, MITTAL R, et al. Computational modelling and analysis of the hydrodynamics of a highly deformable fish pectoral fin[J]. Journal of Fluid Mechanics, 2010, 645: 345–373. doi: 10.1017/S0022112009992941 [23] DANOS N, LAUDER G V. The ontogeny of fin function during routine turns in zebrafish Danio rerio[J]. Journal of Experimental Biology, 2007, 210(19): 3374. doi: 10.1242/jeb.007484 [24] WEIS-FOGH T. Quick estimates of flight fitness in hovering animals, including novel mechanisms for lift production[J]. Journal of Experimental Biology, 1973, 59(1): 169–230. doi: 10.1242/jeb.59.1.169 [25] YANG Y, WU G H, YU Y L, et al. Two-dimensional self-propelled fish motion in medium: an integrated method for deforming body dynamics and unsteady fluid dynamics[J]. Chinese Physics Letters, 2008, 25(2): 4. [26] FOREMAN M B, EATON R C. The direction change concept for reticulospinal control of goldfish escape[J]. Journal of Neuroscience the Official Journal of the Society for Neuroscience, 1993, 13(10): 4101–13. doi: 10.1523/JNEUROSCI.13-10-04101.1993 [27] WANG Z W, YU Y L, TONG B G. An energetics analysis of fish self-propelled swimming[J]. Science China, 2018, 61(7): 4. [28] WANG Z W, YU Y L. Energetics comparison between zebrafish C-shaped turning and escape: self-propelled simulation with novel curvature models[J]. Journal of University of Chinese Academy of Sciences, 2019, 36(4): 467–480. -
点击查看大图
计量
- 文章访问数: 14
- HTML全文浏览量: 16
- PDF下载量: 3
- 被引次数: 0
