0   引言

当液体中加入表面活性剂后，由于表面活性剂分子的存在，液体的表面张力降低，可以形成比一般液膜更稳定、更薄的皂膜。皂膜已经被广泛应用于实验研究，例如，Cohen等^[1]研究了重力作用下超大皂膜泡的形状，并据此提出了类似帐篷、气膜馆等膨胀结构的一种优化外形；Couder等^[2]开创性地提出利用平面皂膜模拟二维流动；Chomaz等^[3]系统分析了平面皂膜流动与二维流动的相似性。皂膜流动还被广泛应用于研究二维绕流^[4-6]、湍流流动^[7-17]以及流固耦合等问题^[18]；此外，由于皂膜中的扰动以表面张力控制的表面波形式传播，传播速度较小，容易产生流速大于波速的“超声速”状态，利用皂膜流动这一特点，可以研究激波传播以及超声速流动问题^[19-22]。

国内学者也广泛开展了皂膜流动实验，针对二维流动^[23-24]、流固耦合^[25]、表面张力梯度导致的对流^[26]、表面活性剂对皂膜流动的影响^[27-28]以及皂膜与激波相互作用^[29]等问题进行了研究。

虽然皂膜流动实验已被大量开展，但在单一实验中，极少会对皂膜流动参数进行全面评估。例如，在利用皂膜流动开展二维扰流或二维湍流研究时，其关注点往往仅限于流场，而对其他参数(如皂膜表面张力系数、皂膜厚度等)的影响，通常予以忽略。在利用皂膜进行激波或超声速研究时，表面张力系数通常借用半无限深流体表面张力系数分析的结果，同时假设皂膜厚度均匀^[20]，由此得到一个“声速”，并认为其在皂膜内处处相等。但是，通过红外吸收法测量得到的皂膜厚度显示：即使对于稳定流动，皂膜厚度也并非处处一致，且厚度剖面还会随总流量的变化而变化^[30]。此外，对于皂膜这一类极薄液体层，表面张力系数也取决于皂膜厚度^[2]。在此情形下，很难认为皂膜内的扰动波传播速度是均匀的。

根据界面所处的状态，表面张力系数测量方法主要分为两类：静态测量方法和动态测量方法。前者基于界面上的力平衡间接测量表面张力系数，包括平板法、挂环法、毛细管上升法、体积法和悬滴法等^[31-32]；后者则是在界面动态变化时对其表面张力系数进行测量，包括最大气泡压力法、振动液滴法、振动射流法和气泡射流法等^[33]。这些方法都需要另外构造实验装置，并不是流动皂膜的直接测量方法。

本文基于皂膜边界上的力平衡严格推导了竖直皂膜的边界形状方程，证明了新近文献中的一个半经验公式^[34]，并提出了一种新的、更简便易行的皂膜表面张力系数测量方法。对于流动皂膜的厚度，一般采用光学手段进行测量(比如利用皂膜对多个波长可见光的干涉^[35-36]，或利用皂膜对特定波长红外辐射的吸收)，并假定皂膜和水的吸收特性一致^{[30, 37]}。本文结合测得的速度剖面，发展了一种新的皂膜厚度的干涉测量法，在不需假定皂膜吸收特性的前提下以单个波长光源实现厚度测量。在自主搭建的重力驱动平面流动皂膜实验装置上，利用本文提出的方法测量了皂膜的表面张力系数、厚度和流动速度。

1   重力驱动平面流动皂膜实验装置

搭建的平面流动皂膜实验装置如图 1所示。参考文献[12-13]，并经反复尝试，本文采用质量比为2:10:88的Dawn牌商用洗碗液+甘油+去离子水混合配制皂液。洗碗液中含有表面活性剂十二烷基硫酸钠，可以降低水的表面张力系数，使皂膜富有弹性，从而具有一定的抗干扰能力^[27-28]；甘油可以增强混合液的黏性，减缓皂膜内部相对运动，使之更加稳定。

图  1  竖直平面流动皂膜实验装置图

Fig.  1  Schematic drawing of the vertical planar soap-film flow experimental device

下载: 全尺寸图片 幻灯片

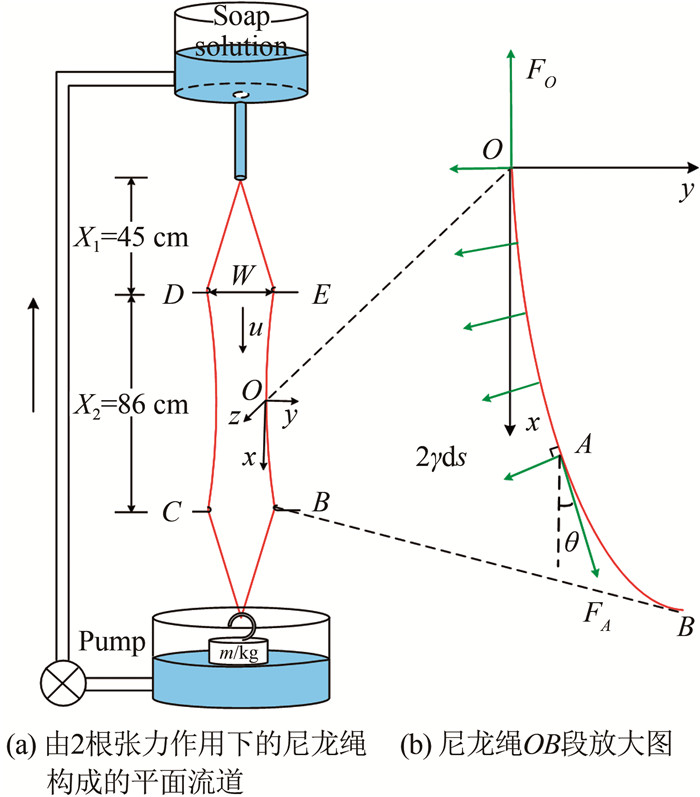
如图 1(a)所示，配制的皂液盛于上水箱中，经一个狭长的出水管流出，进入一个由两根直径为0.32 mm的尼龙绳构成的竖直平面流道(实验中，尼龙绳一直处于下方砝码施加的张力作用下)。紧接出水管口的流道为渐扩的扩张段，其下为流道宽度不变的实验段和流道逐渐收窄的收缩段(在本文实验中，扩张段长度X₁=45 cm；实验段长度X₂=86 cm，实验段入口宽度W=5 cm)。在扩张段，皂液在重力驱动下加速，当重力和空气阻力平衡时充分发展，最终在实验段达到匀速运动，之后经收缩段流入下水箱，再被泵回至上水箱，形成往复循环。

实验启动时，两根尼龙绳贴合在一起；尼龙绳被皂液完全浸润后，缓慢向两侧移动B、C、D和E点的挂钩，分开尼龙绳至指定宽度，在两绳之间形成稳定流动的皂膜。皂膜的平均速度和平均厚度可以通过调节泵的流量加以控制。当泵的流量Q=5~60 mL/min时，可以得到平均速度u=1~4 m/s、平均厚度h=3~9 μm的稳定竖直流动的平面皂膜。

下文对该平面流动皂膜进行力平衡分析，并由此推导出一种测量皂膜表面张力系数的方法；利用激光干涉法测量皂膜厚度，并简要介绍皂膜速度的测量。

2   皂膜表面张力系数测量

由于皂膜厚度很小，其表面张力系数不能简单采用对半无限深液体表面张力系数分析的结果^[2]。Sane等^[34]通过皂膜的力平衡分析得到一种测量皂膜表面张力系数的简便方法，但在推导中多处采用了近似方法。本文给出一个严格推导，得出确切结论，并通过后文介绍的平面流动皂膜测量结果对该结论进行检验，证明推导的正确性；在此基础上，计算皂膜的表面张力系数。

如图 1(a)所示，尼龙绳BE和CD下方悬挂质量为m的砝码以施加张力、保持流道稳定。当没有皂液流动时，尼龙线BE和CD在砝码作用下保持铅直；当皂液流入流道形成皂膜，尼龙绳BE和CD在皂膜表面张力的作用下向皂膜侧略微收缩，形成微微内凹的流道(图中对内凹程度有所放大)。从力平衡的角度出发，推导出该内凹曲线的形状与皂膜表面张力系数的关系，可以给出一种测量流动皂膜表面张力系数的方法。

选取尼龙绳BE的中点O为坐标系原点，x轴为重力方向。设A为尼龙绳OB段上任一点，坐标为(x_A, y_A)，对尼龙绳段OA进行受力分析。简单的受力大小估计表明：当皂膜流向方向的尺寸在1 m量级、砝码自重在1 kg量级时，尼龙绳自重、流动皂膜对尼龙绳的动压力、黏性力等都至多为尼龙绳张力的1/10⁴，在后续分析中忽略它们对尼龙绳力平衡的影响。因此，尼龙绳受到点O、点A的拉力F_O、F_A以及尼龙绳上各微元段ds=dx/cosθ(x)的表面张力，其中，θ(x)表示尼龙绳上一点x处切向方向与重力方向的夹角。由于对称性，在中点O处θ(0)=0。因此，尼龙绳段OA在水平和竖直方向的受力平衡关系式分别为：

在推导式(1)和(2)时，假设皂膜边界上的表面张力系数γ不随位置而变化(对于充分发展达到稳定流动的皂膜，此假设是合理的)；式中的系数“2”是考虑到皂膜前后表面都会对尼龙绳产生表面张力。

将式(1)和(2)相除，并注意到点A的任意性，可以得到描述流道内凹形状的曲线方程：

对式(3)积分，并结合边界条件y(x=0)=0，得到曲线方程如下：

式(4)中包含未知参数F_O(即尼龙绳中点O处的拉力)，其值可以通过将式(2)应用于B点，并代入B点处尼龙绳的力平衡关系F_Bcosθ(x_B)=mg/2得到：

式中，L为BE段尼龙绳长度，推导式(5)时使用了x_B=L/2。式(4)可稍加整理为：

其中，参数2γL/F_O的值为：

式(6)和(7)即为边界曲线形状的准确方程。在推导方程的过程中，除物理上的简单假设(如忽略尼龙绳自重)外，未作任何数学上的近似。

与悬挂物(砝码)的重力相比，表面张力通常很小。例如，当L=1 m、m=1 kg时，取纯水的表面张力系数γ=72 mN/m，得到2γL/(mg)≈1.5×10^-2，代入式(7)得到2γL/F_O≈3.0×10^-2。记ε=2γL/F_O，ε′=2γL/(mg)，则ε和ε′为同阶远小于1的小量。因此，对式(6)关于ε进行小参数展开可得：

式(8)表明：流道边界曲线方程可以很好地用抛物线来近似(因为下一阶修正项为ε³项)，并且给出了确切的系数，可以据此测出皂膜的表面张力系数。在实际应用中，可以利用ε′≪1对其进一步简化得到：

或

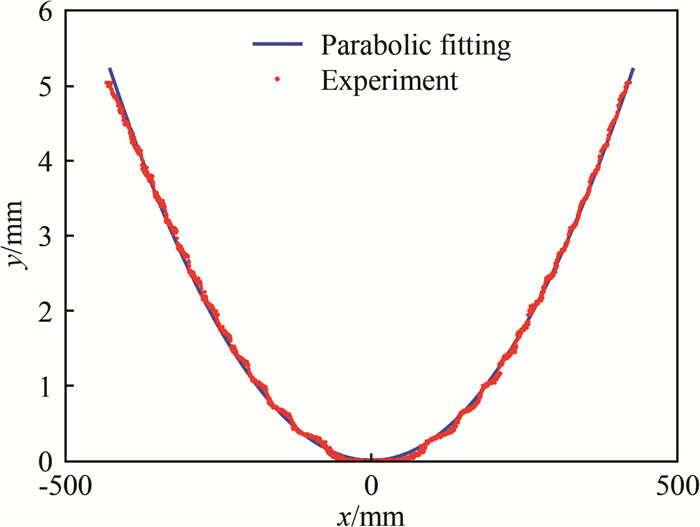
为验证曲线方程(10)，在砝码质量m=0.2 kg、皂液流量Q=35 mL/min时，实测了稳态流动皂膜状态下尼龙绳的位置坐标，如图 2中的离散点所示。尼龙绳位置通过照相得到，为获得较大范围内的图像，采用的放大倍数为1个像素对应0.35 mm的物理尺寸。对尼龙绳图像在水平方向的光强分布进行高斯函数拟合以获得亚像素的定位精度^[38]。图 2中的光滑曲线是采用式(10)进行拟合的结果，与实测曲线吻合良好，验证了分析的正确性。利用已知的砝码质量，可以进一步得到表面张力系数γ=27.5 mN/m。值得注意的是：当砝码质量很小时，表面张力引起的流道收缩很大(在中点O处达到最大值12%)，为避免由此带来的流速和厚度场改变，在流动皂膜实验中一般使用m=2 kg的砝码。

图  2  流道边界实测值(红色点)与理论分析(蓝色线)对比

Fig.  2  Comparison of the measured channel boundary (red dots) and the theoretical prediction (blue line)

下载: 全尺寸图片 幻灯片

Sane等^[34]推导了表面张力系数与尼龙绳曲线方程的关系，但并未获得曲线方程的精确解，而是采用高阶多项式对实测曲线进行拟合，发现选取二阶多项式可以得到较好的结果，从而也获得了式(10)，并通过拟合系数得到了表面张力系数。本文的严格推导说明：流道边界曲线是抛物线加上高两阶小量的修正。图(2)也证明了这一推导结论的正确性。

采用测量边界曲线形状的方式来获得表面张力系数，在实验上存在一处困难：通常边界曲线曲率较小，为测出其具体形状必须拍摄较大范围；对于幅面大小一定的相机，这意味着空间分辨率的降低，给准确确定边界曲线带来了一定困难。因此，本文提出一种新的、更简便易行的表面张力系数测量方法。

根据式(10)，可以给出流道中点O在有皂膜流动时相对于无皂膜流动时(即尼龙绳为竖直状态时)的位移：

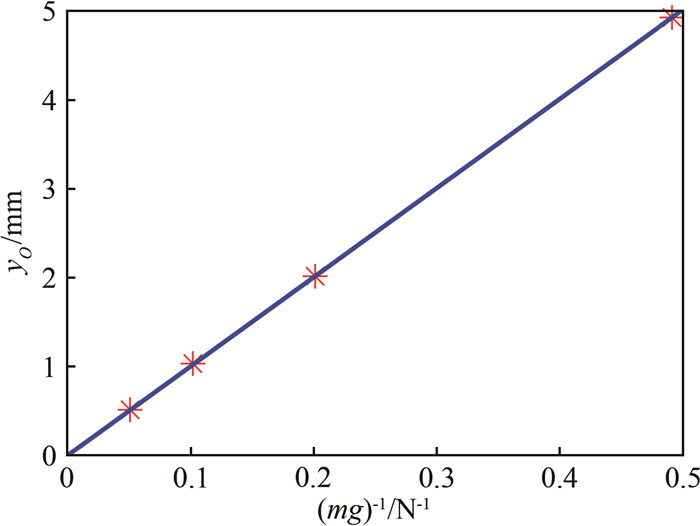
因此，通过测量给定砝码质量下流道中点O的位移，就可以很方便地使用式(11)得到皂膜的表面张力系数。此方法的一个优点是：无需拍摄大范围的尼龙绳图像，照相时可以采用较大的放大倍数，获得较高的空间分辨率。在实际应用时，本文采用了每像素对应0.01 mm物理尺寸的分辨率。根据式(11)，γ≈2mgy_O/L²，砝码质量m=(500±1) g和尼龙绳长度L=(500±1) mm的测量都可以控制在0.2%的测量偏差范围内。当y_O=(1±0.01) mm的测量偏差范围降低至1%，实现了仅有2%左右不确定度的表面张力系数测量。

图 3给出了在同一皂液流量Q = 35 mL/min下测得的流道中点O的位移随砝码质量的变化以及根据式(11)拟合的直线。所有数据点都很好地落在过原点的拟合直线上，进一步验证了本文推导的正确性。根据直线斜率测得的表面张力系数γ=27.1 mN/m，与前述抛物线拟合法得到的结果相近。

图  3  流道中点O在有/无皂膜流动时的位移量随砝码质量的变化

Fig.  3  Horizontal shift of the middle point of the channel with the inverse of the hanging weight: measurements (red stars) vs. theoretical prediction (blue line)

下载: 全尺寸图片 幻灯片

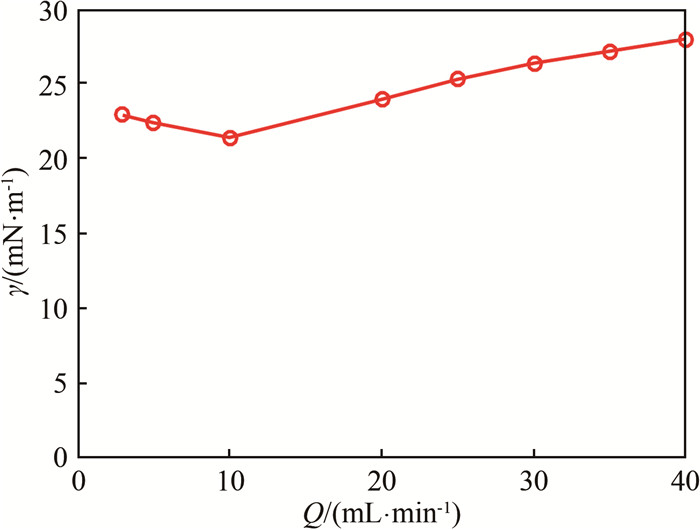
利用这一方法，还测量了表面张力系数随皂液流量的变化关系，如图 4所示。图中曲线并非如部分文献报道的“表面张力系数随皂液流量增加而单调下降”^[34]，这可能是由于表面张力系数随皂膜厚度变化而有所变化^[2]、且实验中皂膜厚度并非均匀分布导致的。

图  4  表面张力系数随皂液流量的变化

Fig.  4  Change of the surface tension coefficient with the flow rate of the soap film

下载: 全尺寸图片 幻灯片

3   皂膜厚度测量

对流动皂膜的厚度场进行测量，无法采用接触式方法，主要采用光学测量手段，比如利用皂膜对不同波长可见光的干涉^[35-36]，或利用皂膜对特定波长红外辐射的吸收^{[30, 37]}。本文提出一种与速度场测量相结合的、基于薄膜干涉的光学测量方法。

如图 5所示，在波长为λ=532 nm的单色激光照射下，流量Q=40 mL/min的皂膜表面形成了明暗相间的干涉条纹。可以发现：干涉条纹基本为竖直条纹，表明皂膜厚度在水平方向的变化远大于在竖直方向的变化，即，对于竖直方向流动的稳定皂膜，水平方向的质量输运很弱，厚度在竖直方向上几乎不变。另外，皂膜边界几乎处于同一竖直干涉条纹上，说明其厚度变化很小，由于厚度不同而可能导致的表面张力沿边界的变化也很小，这也间接支持了前文作出的边界处表面张力相同的假设。本文忽略竖直方向的皂膜厚度变化，仅分析水平方向的厚度变化造成的干涉现象。

图  5  皂膜表面干涉条纹

Fig.  5  Interference fringes produced by a laser beam reflected from the soap-film

下载: 全尺寸图片 幻灯片

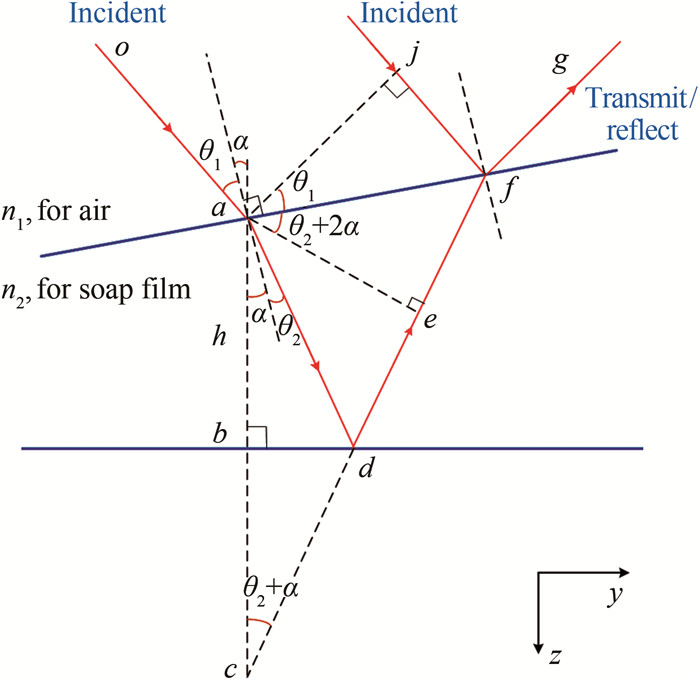
图 6为皂膜横剖面内的光路图，上、下蓝线分别表示z方向的皂膜前后表面。平行光oa和jf以入射角θ₁入射至皂膜的前表面af，由于空气折射率n₁和皂液折射率n₂不同，入射光在前表面af发生折射及反射；oa的折射光ad到达皂膜的后表面bd后，再次发生折射与反射，考虑其反射光df恰好到达f点，将与入射光jf发生叠加，其结果取决于光线o-a-d-f与j-f的光程差。

图  6  皂膜横剖面内的光路图

Fig.  6  Incident and reflected laser light paths in a horizontal cross-section of the soap-film

下载: 全尺寸图片 幻灯片

记皂膜在a点的厚度为h(y=a)=ab，则在f点的光程差OPD(Optical Path Difference)为Δl：

记光线在a点的折射角为θ₂，则：

其中，α=arctan(∂h/∂y)为皂膜外法线与z方向的夹角。将式(13)和(14)代入式(12)，可得：

其中，最后一个等式是基于α≈Δh/Δy≈1×10^-4而作的简化。值得注意的是，当光从低折射率n₁的空气入射到高折射率n₂的皂膜中，会发生180°的相位变化^[39]，因此，当Δl=(k－0.5)λ, k=1, 2, 3, …时会产生相长干涉，而当Δl=kλ, k=1, 2, 3, …时则会产生相消干涉。

根据式(15)，干涉条纹可以提供沿y方向皂膜厚度的相对变化情况。相邻的两个明条纹(暗条纹)光程差为λ，对应的厚度变化为δh=λ/(2n₂cosθ₂)。假设尼龙绳边界处皂膜厚度为h(y=0)=h₀，则根据流动皂膜的质量守恒可得：

其中，δh(y)=h(y)－h₀为皂膜内部一点处与边界处的相对厚度，可通过干涉条纹的个数及插值计算得出。因此，对于给定的皂液流量Q，若实验测得皂膜水平截面上的速度剖面u(y)，则可以通过式(16)确定边界处的厚度h₀，进而获得皂膜水平方向的厚度剖面h(y)。

采用粒子图像测速法(Particle Image Velocimetry, PIV)对皂膜的速度场进行测量。在皂液中加入直径1 μm的聚苯乙烯塑料珠作为流动示踪颗粒，以重复频率5000 Hz、功率100 W的高频高功率脉冲激光照亮示踪颗粒，通过与激光器同步的高速相机拍摄瞬时颗粒图像，再采用标准的互相关算法来获取流动速度剖面h(y)。

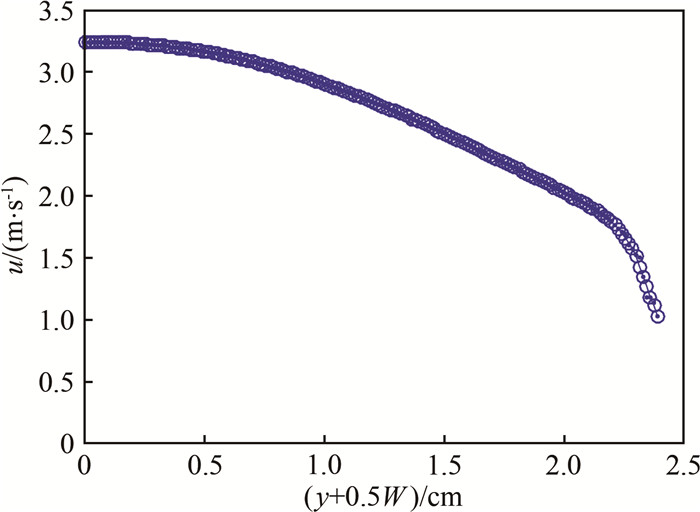
图 7为x=0处(即实验段中心位置)、皂液流量Q=35 mL/min时的皂膜流动速度剖面(仅显示对称的右半部分剖面；在表面张力的拉伸作用下，x=0处的皂膜宽度略小于实验段入口处宽度5 cm，约为4.85 cm)。从图中可见，皂膜速度在中心处较大，而在靠近边界处(尼龙绳处)速度较小。

图  7  皂膜流动的速度剖面

Fig.  7  Profile of the vertical velocity of the soap-film flow

下载: 全尺寸图片 幻灯片

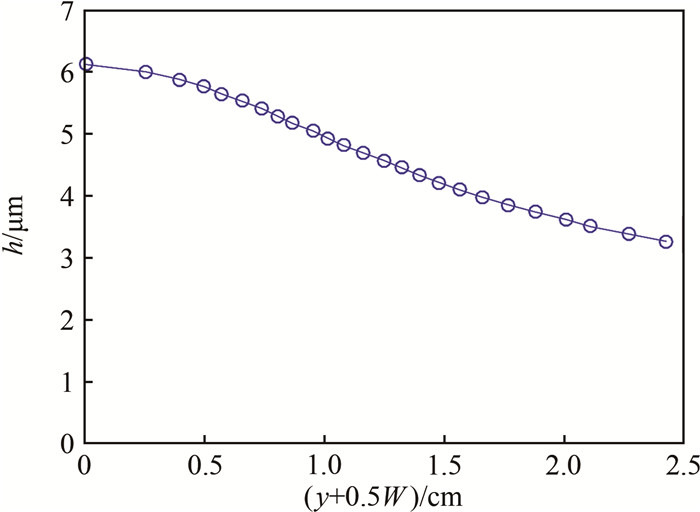
根据实测的速度剖面，利用式(15)计算得到的皂膜厚度剖面如图 8所示(仅显示右半部分剖面)。可以看出，类似于速度剖面，皂膜厚度在中心处较大，向边界处逐渐变薄。在本文实验工况下，测得的皂膜内平均速度u=1~4 m/s，皂膜平均厚度h=3~9 μm，这与Wu等^[30]针对类似流动皂膜进行测量的结果基本一致。

图  8  皂膜流动的厚度剖面

Fig.  8  Profile of the thickness of the soap-film flow

下载: 全尺寸图片 幻灯片

4   结论

本文搭建了一个重力驱动的平面流动皂膜实验装置，能够得到皂液流量Q=5~60 mL/min、平均速度u=1~4 m/s、平均厚度h=3~9 μm的稳定竖直流动的皂膜。为测量皂膜的表面张力系数，基于皂膜边界上的力平衡方程推导得到流动皂膜边界曲线方程的精确解。实验结果验证了本文推导，并由此得出表面张力系数的两种测量方法。此外，还提出了一种基于光学干涉的皂膜厚度测量方法。将该方法与皂膜流动速度剖面测量相结合，可以给出皂膜的厚度剖面。本文中提出的皂膜表面张力系数及厚度的测量方法简便易行，可以较为全面地测量平面流动皂膜并评估其特性(如扰动波在皂膜中的传播速度)。