0   引言

湍流与壁面的摩擦阻力是流体流动阻力的主要来源，通过控制湍流来减小壁面摩擦阻力对于节能减排具有重要的意义和应用价值。沟槽壁面减阻和超疏水壁面减阻作为2种典型的被动控制减阻技术，具有不需要额外能量消耗、控制简单易行、减阻效果显著等优点，一直受到学术界和工业部门的重视。

在沟槽减阻方面，Bechert等^[1]通过油洞实验对各种沟槽结构单元体的阻力性能进行研究，发现Blade型减阻效果最好，减阻率可达9.9%。Chamorro等^[2]对表面覆盖有纵向微沟槽的机翼模型进行模拟研究，发现微沟槽的尺寸对其减阻效果有很大影响。Mamori等^[3]对正弦型沟槽表面在湍流通道流中的涡旋结构进行测量，发现沟槽内部产生的二次涡可以降低顺流向反向旋转涡对向上抬升低速流体的能力，从而降低湍流猝发。Benschop等^[4]对一种具有防垢性能的沟槽表面进行了实验研究，得到了6%的减阻率。杨绍琼^[5]和李山^[6-7]等发现沟槽改变了相干结构的空间形态和尺度，减少了近壁流体和外区的动量能量交换。王鑫等^[8]的实验结果表明沟槽使得近壁区顺向涡数量和尺度差异均减小，从而实现流动减阻。

超疏水壁面减阻是新发展起来的一种新型仿生减阻技术。这种技术通过模仿荷叶表面微纳尺度结构产生的超疏水效应，利用人工制备超疏水壁面实现湍流减阻，是近年来学术研究的热点。在超疏水减阻方面，Park等^[9]通过实验发现减阻效果与壁面微结构的含气率密切相关。Rastegari等^[10]指出超过80%的减阻是由壁面有效滑移引起的。Gose等^[11]基于高雷诺数研究了4个不同的机械耐用超疏水表面在充分发展的湍流边界层中的减阻特性，发现减阻程度取决于表面精确的形态。Arenas等^[12]对粗糙元上同时覆盖着气层和液层2种流体的槽道湍流进行直接数值模拟，发现2种流体的界面形成的润滑层和覆盖在上面的流体降低了总的阻力，法向脉动速度的大小与总阻力密切相关。Rowin等^[13]对随机凸起产生的超疏水壁湍流进行了研究，发现超疏水壁面的流向和展向速度剖面均高于光滑亲水表面，达到了38%的减阻率。Fairhall等^[14]发现超疏水壁湍流中壁面滑移的直接效应并没有改变壁面上湍流的动力学特性，壁面摩擦阻力是由2个虚拟原点决定的，一个是平均流场的虚拟原点，一个是沟槽湍流的虚拟原点，减阻率正比于这2个虚拟原点之差。北京大学余永生等^[15]对涂有聚四氟乙烯的疏水壁面进行了层流减阻研究，发现减阻效果来源于层流，而非转捩延迟，并认为粗糙表面和疏水涂层共同决定疏水性能。清华大学张静娴等^[16-17]对超疏水壁面的湍流边界层进行实验研究，发现在近壁区由于发卡涡抬升，湍流脉动强度减弱，超疏水表面湍流相干结构更加稳定。胡海豹等^[18]通过数值模拟对超疏水表面在湍流状态下的减阻效果进行了研究，结果表明超疏水表面气液界面处产生了显著的滑移流动，滑移越大，减阻效果越明显。苏健等^[19]发现超疏水壁面减阻效果的发生与逆向涡的存在密切相关。田海平等^[20-21]从壁湍流相干结构控制的角度对超疏水壁面减阻的机理进行实验研究，发现超疏水壁面通过削弱猝发事件的强度及低速条带的尺度实现减阻。刘铁峰等^[22]发现超疏水表面摩擦阻力的减小与其能够使壁湍流中的湍动能向小能量尺度相干结构倾斜密切相关。

由于单一的被动减阻技术的减阻效果有限，因此本文将沟槽壁面与超疏水壁面相结合形成沟槽超疏水复合壁面，利用二者的优势进一步提高减阻效率，并用TRPIV技术测量湍流边界层在沟槽超疏水复合壁面、超疏水壁面以及亲水壁面的瞬时速度场，通过对3种壁面湍流边界层速度场实验数据的对比分析，研究沟槽超疏水复合壁面的减阻机理。

1   实验设备与技术

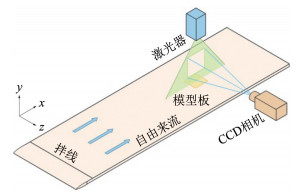
实验在天津大学流体力学实验室重力溢流低湍流度回流水洞中进行。水洞实验段尺寸为4.1 m×0.6 m×0.7 m (长×宽×高), 流速最高达0.5 m/s, 背景湍流度小于1%。实验用大平板尺寸为3.70 m×0.59 m×0.01 m(长×宽×厚)，前缘按8∶1椭圆修形。大平板前缘下游3.3 m处开有凹槽，用于镶嵌尺寸为13 cm×13 cm×1 cm(长×宽×厚)的亲水平板、超疏水平板以及沟槽超疏水平板模型。为了获得充分发展的湍流边界层，在大平板前缘下游200 mm处装有直径d_t=2 mm的拌线。实验装置如图 1所示。在本文中x、y和z分别代表流向、法向和展向，u、v和w分别为流向、法向和展向脉动速度。

图  1  实验装置示意图

Fig.  1  Experimental setup diagram

下载: 全尺寸图片 幻灯片

实验所用亲水、超疏水和沟槽超疏水平板模型的主要制作过程为：选用边长l_m=13 cm的方形铝板，将铝板抛光后放入超声波容器清洗。所有方板的侧面都加工成梯形槽，以镶嵌在大平板的凹槽当中。将其中一块已抛光的光滑板作为亲水壁面，将其表面涂为黑色以减少激光反射，其余板用于制作超疏水和沟槽超疏水复合壁面。

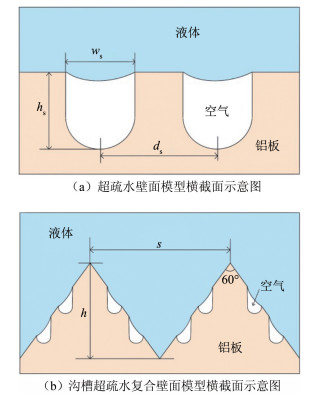
本文利用超快激光刻蚀的方法获得超疏水表面。制备超疏水表面的主要过程为：利用飞秒激光器的高能激光束聚焦而成的极小光斑，在焦点处形成很高的功率密度使材料在瞬间气化蒸发，从而在方形铝板上形成纵向U型微沟槽以构造超疏水表面。激光的加工精度为2 μm，U型微沟槽结构宽w_s=35 μm，深h_s=30 μm，长l_s=120 mm，U型微沟槽结构中心线之间的距离d_s=50 μm，其结构如图 2(a)所示。最后以氟硅烷溶液降低其表面能(关于降低表面能的具体细节详见文献[23])，由此方法获得的超疏水板壁面静态接触角能够达到155°。根据Cassie方程cosθ_c=ϕ_s(cosθ_e+1)-1可算得水与固体表面接触的面积占总表面积的比ϕ_s，式中θ_c=155°为实验的表观接触角，θ_e=108°为铝板氟化处理后的本征接触角，因此ϕ_s=0.125。进而可以知道在超疏水表面上气层的覆盖面积达到了87.5%，而U型微沟槽的面积占整体表面积的比为70%，可以推测出U型微沟槽内的气体是呈现出一定的外溢状态并且附着在固体表面的，能提供良好的超疏水性能。

图  2  实验模型横截面示意图

Fig.  2  Cross-section schematic diagram of the experimental model

下载: 全尺寸图片 幻灯片

关于沟槽超疏水板的制作，考虑到沟槽的强度以及在沟槽表面刻蚀微结构的可行性，先在铝板表面加工出三角形顺流向沟槽，然后重复上述制备超疏水表面的方法，从而得到沟槽超疏水复合壁面。其中三角形顺流向沟槽顶角为60°，槽深h=1.6 mm，沟槽之间的间距s=1.85 mm，其结构如图 2(b)所示。

实验用示踪粒子为直径d_p=20 μm的空心玻璃微珠，粒子密度ρ_p=1.04 kg/m³。实验时自由来流速度U_∞=0.26 m/s，水温T=22 ℃，水的密度ρ=998 kg/m³，动力黏性系数μ=959×10^-6 kg/(m·s)。PIV粒子图像的采集采用的是丹麦Dantec公司的SpeedSense 9072 CCD相机，其分辨率为1280 pixel×800 pixel，对应的物理空间尺寸为88.6 mm×54.6 mm (x×y)，照亮流场的激光片光源的厚度约为1 mm。粒子图像采样频率f_a=400 Hz，自由来流部分的粒子在相邻2帧图像之间的位移约为9 pixel，粒子图像的粒子浓度约为每32 pixel×32 pixel中22个粒子。每个模型以每组记录8215张图像的方式采集3组共24 645张粒子图像，然后采用丹麦Dantec公司的DynamicStudio软件进行数据处理互相关计算。查询窗口大小为32 pixel×32 pixel，窗口重叠率为75%，得到的每个瞬时二维速度矢量场具有156×93 (x×y)个速度矢量，插值的速度矢量占比低于1%，流向及法向上相邻矢量之间的空间间隔d_x=d_y=0.562 mm，速度场测量的相对误差约为1%。

2   实验结果与分析

2.1   湍流基本统计量分析

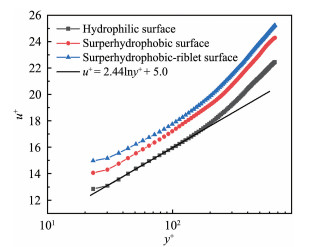
图 3为3种壁面的内尺度无量纲化平均速度沿法向变化的剖面曲线。横轴为y⁺=yu_τ/υ，纵轴为u⁺=u/u_τ，其中u_τ为壁面摩擦速度，υ为水的运动黏性系数。本文利用文献[24-25]所提出的拟合平均速度剖面对数律区的方法得到壁面摩擦速度u_τ，依据对数律公式u⁺=(1/κ)lny⁺+B可得u/u_τ=(1/κ)ln(yu_τ/υ)+B，其中κ为卡门常数，B为积分常数。各种壁面的u_τ，κ与B都通过拟合算出，拟合方式为将对数律区平均速度剖面的实验数据带入f(u_τ, κ, B) , 当f(u_τ, κ, B)取得最小值时的u_τ，κ和B即为所求值。亲水壁面、超疏水壁面和沟槽超疏水复合壁面的κ分别为0.41、0.41和0.40，B分别为5.0、6.4和7.6，各壁面u_τ的值如表 1所示。本文的对数律区范围为法向高度0.18δ(δ为湍流边界层基于0.99U_∞的名义厚度)以下且y⁺>30的部分，数据的拟合误差小于1%。根据壁面摩擦速度与壁面摩擦切应力的关系τ_w=ρu_τ²，结合平均自由来流速度U_∞，可得壁面摩擦系数C_f=2τ_w/ρU_∞²，最终可得减阻率η=(1-C_f*/C_fh)×100%，其中C_f*代表超疏水或沟槽超疏水壁面的摩擦系数，C_fh代表亲水壁面的摩擦系数。表 1列出了3种壁面的基本流动参数以及湍流减阻率。其中Re_τ为内尺度雷诺数，其计算公式为Re_τ=u_τδ/υ。

图  3  平均速度剖面

Fig.  3  Comparison of mean velocity profiles

下载: 全尺寸图片 幻灯片

表  1  基本湍流减阻参数

Table  1  Basic turbulent drag reduction parameters

参数	亲水壁面	超疏水壁面	沟槽超疏水复合壁面
U∞/(m·s-1)	0.26	0.26	0.26
uτ/(m·s-1)	0.0119	0.0110	0.0105
Reτ	621	574	552
τw/(kg·m-1·s-2)	0.140 745	0.120 886	0.109 254
Cf	0.003 965	0.003 388	0.003 144
η		14.6%	20.7%

下载: 导出CSV 

| 显示表格

由图 3可以看出，在同一法向高度，沟槽超疏水复合壁面、超疏水壁面与亲水壁面的内尺度无量纲化平均速度依次降低。超疏水壁面和沟槽超疏水复合壁面相比于亲水壁面缓冲层增厚，对数律区依次上移，速度剖面上移，这与前人研究结果一致^[22]。沟槽超疏水复合壁面的减阻效果优于单一的超疏水壁面，在表 1中计算的减阻率中也有所体现。

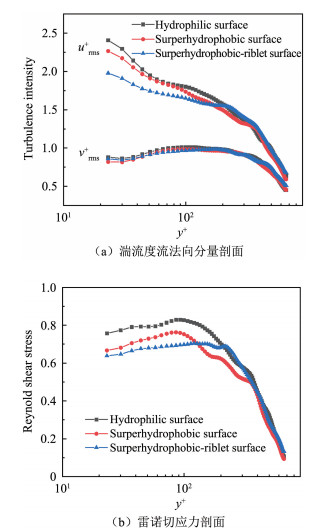
由于不同壁面的壁面摩擦速度不一致，因此为了便于比较分析, 下文统一采用平板的壁面摩擦速度进行内尺度无量纲化。图 4(a)为速度场中部3种壁面的流向及法向的湍流脉动强度随y⁺的变化曲线，图中u_rms⁺和v_rms⁺分别代表内尺度无量纲化的流向及法向脉动速度均方根值。从图中可以看出，在y⁺ < 150时超疏水壁面和沟槽超疏水复合壁面的流向湍流脉动强度相对亲水壁面呈依次减弱趋势，其中沟槽超疏水复合壁面的流向湍流脉动强度减弱幅值最大，在y⁺ < 30的缓冲层其流向湍流脉动强度减弱的相对幅值接近20%。而3种壁面的法向脉动强度差距不大，因此从图中可以看出超疏水壁面上的U型微沟槽主要对湍流边界层中y⁺ < 150的区域的流向湍流脉动存在抑制作用，而沟槽超疏水复合壁面上的流向沟槽对流向湍流脉动的抑制作用起到了进一步加强的作用。

图  4  湍流度和雷诺切应力剖面

Fig.  4  Turbulence intensity and Reynold shear stress profiles

下载: 全尺寸图片 幻灯片

图 4(b)为相应的雷诺切应力曲线。在y⁺ < 150时亲水壁面、超疏水壁面和沟槽超疏水复合壁面的雷诺切应力依次减弱，与流向湍流脉动强度在不同壁面之间的变化一致，进一步表明在y⁺ < 150时沟槽超疏水复合壁面对湍流脉动的抑制效果优于超疏水壁面。在y⁺≈100时平板壁面、超疏水壁面达到了雷诺切应力的峰值，而沟槽超疏水复合壁面的雷诺切应力峰值则在y⁺≈200处并且开始与亲水壁面趋于一致，表明沟槽超疏水复合壁面在y⁺>100时出现了对湍流脉动抑制效果的衰减，且衰减程度高于超疏水壁面，因此出现150 < y⁺ < 350时超疏水壁面的雷诺切应力最小的情况。

2.2   尺度分解

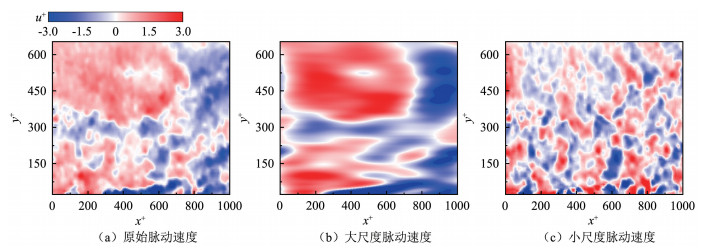
一般认为湍流边界层中的湍流脉动能量是由大尺度结构向小尺度结构传递^[26]。近年来, 学术界发现湍流边界层中大尺度脉动对小尺度脉动存在调制作用，即当大尺度湍流脉动为正时, 小尺度湍流脉动强度会增强，而当大尺度湍流脉动为负时, 小尺度湍流脉动强度会减弱^[27]。因此, 为了进一步研究超疏水壁面和沟槽超疏水复合壁面对不同尺度的湍流脉动的影响，本文将瞬时的脉动速度场分解为大尺度部分与小尺度部分。常见的尺度分解方法有小波分解、POD分解、空间滤波等。本文采用基于空间傅里叶变换的空间滤波方法，首先将脉动速度沿流向进行傅里叶变换，而后在波数空间内以λ_x作为截断波长(λ_x/δ=1)，直接将原始脉动速度信号中波长小于λ_x部分的幅值设为0；然后进行反傅里叶变换，取其实部为相应的大尺度脉动信号，而波长小于λ_x的部分则为相应的小尺度脉动信号。图 5(a)为亲水壁面下随机选取的一个瞬时流向脉动速度的等值线图，图 5(b)和(c)为分解后相应的大、小尺度流向脉动速度等值线图，其分解结果与Hutchins等^[27]采用泰勒冻结假设对热线风速仪的时间速度信号作尺度分解的结果一致。

图  5  不同尺度的脉动速度

Fig.  5  Fluctuation velocity of different scales

下载: 全尺寸图片 幻灯片

2.3   大小尺度湍流脉动强度

图 6为尺度分解后的大、小尺度湍流脉动强度。从图 6(a)中可以看出，大尺度流向湍流脉动强度的变化趋势与图 4一致，但是相应的幅值有所减小。而图 6(b)中超疏水壁面和沟槽超疏水复合壁面的小尺度流向湍流脉动强度只有在y⁺ < 100时才存在明显的减弱，且减弱的差值随着y⁺的增加而快速减小，而小尺度法向湍流脉动强度在不同壁面时无明显变化。但是当y⁺>100时，不同壁面的小尺度流向湍流脉动强度和法向湍流脉动强度都快速地趋于一致。对比图 6和图 4可以看出，流向湍流脉动强度的大尺度成分占比较高，而法向湍流脉动强度的小尺度成分占比较高。超疏水壁面和沟槽超疏水复合壁面对大尺度流向湍流脉动强度的抑制作用可以到达y⁺=150的法向位置，而对小尺度流向湍流脉动强度的抑制作用只能到达y⁺=100的法向位置，法向湍流脉动强度则不受壁面影响。

图  6  分尺度湍流脉动强度

Fig.  6  Turbulence fluctuation intensity of different scales

下载: 全尺寸图片 幻灯片

2.4   大尺度脉动速度条件相位平均

湍流边界层中的大尺度湍流脉动主要是由沿流向排列的发卡涡包向下游迁移过程中在发卡涡包内部由发卡涡头的联合诱导作用产生的大尺度低速流体与上游的高速流体相碰撞导致，也就是通常所说的Q2与Q4事件^[26]。近年来，研究发现大尺度Q2与Q4事件除了对近壁区小尺度湍流脉动强度产生抑制和促进作用外，还能对近壁区的涡结构运用产生类似的调制作用^[27]。由于壁面摩擦阻力与近壁区的雷诺切应力直接关联^[28-29]，而涡结构运动是近壁区雷诺切应力的主要来源，因此大尺度Q2与Q4事件对壁面摩擦阻力的产生具有重要影响。

为了研究不同壁面情况下大尺度湍流脉动与涡结构的变化，本文采用基于展向涡的条件相位平均方法，以0.1δ处的展向涡为条件，对此处的大尺度湍流脉动速度场进行相位平均。展向涡的识别采用的是Λ_ci准则^[30]，Λ_ci=λ_ciω_z/|ω_z|表示流体旋转的强度，其中λ_ci为速度梯度张量复特征值的虚部，ω_z为展向涡量。条件相位平均公式为：

其中，u_L为大尺度脉动速度，由于发卡涡为顺向涡，其Λ_ci为负值，因此条件相位平均后的速度场表示的是发卡涡涡头附近的大尺度脉动速度的平均值。

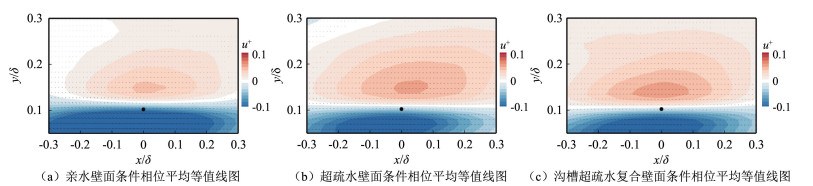
图 7为亲水壁面、超疏水壁面以及沟槽超疏水复合壁面在y_ref=0.1δ时的大尺度流向脉动速度的条件相位平均值。图中的矢量箭头为相应的速度场，黑色圆点标记的是相位平均的参考点位置。从图中可以看出，大尺度流向脉动速度在参考点上部是正向脉动，在参考点下部是负向脉动。其中，正向脉动幅值在亲水壁面、超疏水壁面以及沟槽超疏水复合壁面上依次增大；而负向脉动幅值依次减小，且流向脉动幅值为0的等值线相对参考点的位置在不同壁面上均偏上，亲水壁面的偏离程度最大，超疏水壁面次之，沟槽超疏水复合壁面偏离最低。0等值线与参考点之间的偏离是由顺向涡对下方流体的诱导作用使Q2与Q4的交界面上抬导致^[31]，这表明超疏水壁面与沟槽超疏水复合壁面在近壁区对顺向涡的诱导作用能够产生抑制效果，且沟槽超疏水复合壁面效果更为明显。

图  7  y_ref=0.1δ时大尺度流向脉动速度条件相位平均等值线图

Fig.  7  Conditional phase average contour of large scale streamwise fluctuating velocity condition at y_ref=0.1δ

下载: 全尺寸图片 幻灯片

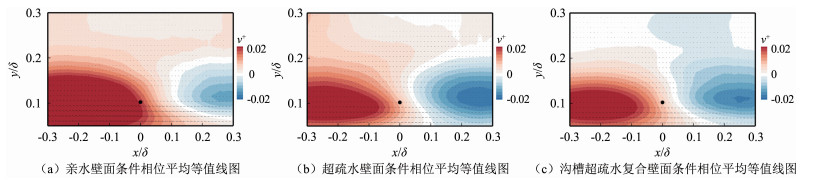
超疏水壁面与沟槽超疏水复合壁面在近壁区对顺向涡本身的运动也存在显著的抑制效果。图 8为亲水壁面、超疏水壁面以及沟槽超疏水复合壁面在y_ref=0.1δ时的大尺度法向脉动速度的条件相位平均值。图中参考点左边为正的脉动，右面为负的脉动，正的脉动幅值在亲水壁面、超疏水壁面以及沟槽超疏水复合壁面依次减小，负的脉动幅值依次增大，这种变化趋势正好与流向脉动幅值相反。而法向脉动幅值为0的等值线相对参考点的位置在不同壁面上都偏右，且偏离程度依次减小，这种减小的趋势与流向脉动幅值的0等值线相一致。这表明超疏水壁面与沟槽超疏水复合壁面对顺向涡的向上运动也具有抑制作用，且沟槽超疏水复合壁面的抑制效果更强，该结果符合附着涡模型的假设^[32]。

图  8  y_ref=0.1δ时大尺度法向脉动速度条件相位平均等值线图

Fig.  8  Conditional phase average contour of large scale normal fluctuating velocity condition at y_ref=0.1δ

下载: 全尺寸图片 幻灯片

从图 6可看出，在超疏水壁面与沟槽超疏水复合壁面上，大尺度流向脉动强度在y⁺ < 150或者y < 0.24δ时相对于亲水壁面呈减弱趋势，大尺度法向脉动强度则几乎不变；但是基于顺向涡的条件相位平均结果，却出现正的大尺度流向脉动与负的法向脉动增强、负的大尺度流向脉动与正的法向脉动减弱。这表明顺向涡向Q2与Q4事件之间的滞止线上游即Q4事件一侧移动，且在沟槽超疏水复合壁面上移动趋势最弱，说明顺向涡的活动强度受到了明显抑制，因此相应的发卡涡包对大尺度脉动的产生强度出现减弱。

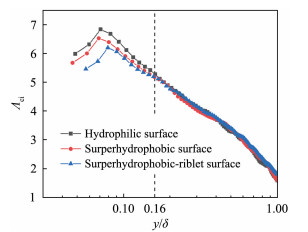
图 9为3种壁面下顺向涡的强度值Λ_ci随法向的变化。从图中可以看到，在y < 0.16δ时3种壁面的涡强度值都呈先增大后减小的趋势，而在同法向高度位置上, 亲水壁面、超疏水壁面以及沟槽超疏水复合壁面的涡强度值则依次减弱，这进一步说明了超疏水壁面以及沟槽超疏水复合壁面对近壁区的涡结构运动存在抑制作用。因此，超疏水壁面以及沟槽超疏水复合壁面通过减小近壁区的发卡涡以及发卡涡包结构的活动来减弱大尺度湍流脉动的强度，进而通过大尺度湍流脉动对小尺度湍流脉动的调制作用来减小小尺度湍流脉动的强度，从而实现壁面减阻。

图  9  顺向涡强度

Fig.  9  Prograde vorticity strength

下载: 全尺寸图片 幻灯片

超疏水壁面的减阻效果主要是由壁面滑移引起，沟槽壁面的减阻效果则由沟槽内部的二次涡对外部湍流边界层近壁区高低速条带结构运动的抑制导致。沟槽超疏水复合壁面同时具有超疏水壁面与沟槽壁面的结构特性，而在沟槽超疏水复合壁面沟槽内部的二次涡流动与壁面之间出现滑移之后，其本身的特点以及对外部湍流边界层的近壁区高低速条带结构的影响还需开展进一步的实验研究。

3   结论

本文通过实验研究发现，在湍流边界层中沟槽超疏水复合壁面的减阻率能够达到20.7%，而超疏水壁面只有14.6%。通过进一步对比分析湍流边界层在亲水壁面、超疏水壁面以及沟槽超疏水复合壁面的速度场，可以得出以下结论：

1) 在y⁺ < 150区域的同一法向高度上，流向湍流脉动强度在沟槽超疏水复合壁面上相对于亲水壁面的减小程度比超疏水壁面更高，而法向湍流脉动强度在3种壁面上无明显变化。

2) 超疏水壁面和沟槽超疏水复合壁面对大尺度流向湍流脉动强度的抑制作用可以到达y⁺=150的法向位置，而对小尺度流向湍流脉动强度的抑制作用只能到达y⁺=100的法向位置。

3) 以顺向涡为条件采样时，在y_ref=0.1δ处超疏水壁面和沟槽超疏水复合壁面的大尺度脉动速度场相比于亲水壁面都出现参考点上方正的大尺度流向脉动速度增强、下方负的大尺度流向脉动速度减弱、左方正的大尺度法向脉动速度减弱、右方负的大尺度法向脉动速度增强。

4) 流向脉动速度为0的等值线相对参考点向上偏离的趋势以及法向脉动速度为0的等值线相对参考点向右偏离的趋势在亲水壁面、超疏水壁面和沟槽超疏水复合壁面上依次减弱。

5) 同法向高度上亲水壁面、超疏水壁面以及沟槽超疏水复合壁面的顺向涡强度值依次减弱。

6) 沟槽超疏水复合壁面比超疏水壁面能更有效地抑制近壁区涡结构的运动，从而减弱湍流脉动的强度，实现更好的减阻效果。